
INTRODUCCIÓN
La envolvente convexa, también denominada cierre convexo o convex hull, es uno de los más fundamentales constructores geométricos.
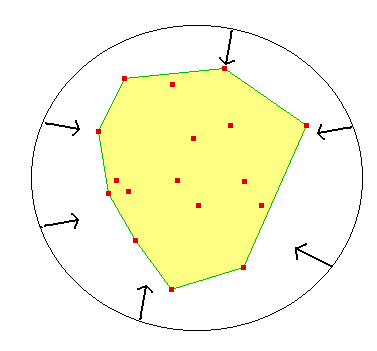
Una idea intuitiva del significado del cierre convexo es el contenido de la figura que formaría una banda elástica que rodeara a una nube de puntos una vez que la soltáramos.
El problema de computar un convex hull no sólo está centrado en aplicaciones prácticas, sino también es un vehículo para la solución de un número de cuestiones aparentemente sin relación con él, que surgen en la Geometría Computacional.
La computación del cierre convexo de una nube finita de puntos, especialmente en el plano, ha sido exhaustivamente estudiada y tiene aplicaciones, como por ejemplo, en el procesado de imágenes y en localización.
Desafortunadamente, no es posible construir la definición intuitiva de cierre convexo citada anteriormente de forma natural, por lo que hay que identificar las nociones apropiadas que nos conduzcan a un algoritmo.
DEFINICIONES
Definición: Un conjunto S se dice convexo si dado cualquier par de puntos x, y pertenecientes al conjunto se cumple que el segmento xy que forman está contenido en dicho conjunto S.
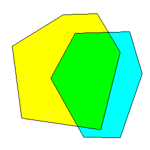
Lema: La intersección formada por cualquier grupo de conjuntos convexos dará como resultado un único conjunto que además también será convexo.
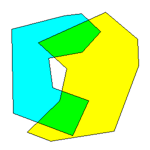
En cambio, como puede verse en la siguiente imagen, la intersección de conjuntos no convexos no tiene por que dar como resultado un conjunto único.
Definición: Dado un conjunto de puntos finito S, se dice que CH(S) es la envolvente o cierre convexo de S si:
- CH(S) es convexo.
- S está contenido en CH(S).
- CH(C) es el menor convexo que contiene a S.
(NOTAS)
- Esta definición se puede extender para conjuntos infinitos, aunque no es el caso que nos interesa.
- Los puntos de la frontera de la envolvente convexa se llaman vértices o extremos de la envolvente convexa, pero también se les suele denominar, de forma poco afortunada, con el mismo nombre de envolvente convexa.
- La envolvente convexa de una nube de puntos es siempre un polígono.
Corolario: Sea S un conjunto. Se cumple que la intersección de todos los convexos que contienen al conjunto S es igual al cierre convexo de S.
Demostración:Sea IC(S) la intersección de todos los convexos que contienen a S.
El cierre convexo de S, CH(S), es un convexo y por ello forma parte de todos los convexos que contienen a S. Además es el menor convexo que contiene a S, por definición de la envolvente convexa.
Por el lema de la intersección de convexos resulta que IC(S) es un convexo, ya que es la intersección de otros convexos.
Como IC(S) contiene a S, está contenido en el menor convexo que contiene a S, que es el cierre convexo de S.
ALGORITMOS
Hay muchos métodos para el cálculo del cierre convexo, ya sea para dos, tres o más dimensiones. Nosotros analizaremos sólo algunos algoritmos para averiguar el convex hull de puntos situados sobre dos dimensiones.
Teorema: Es posible calcular la envolvente convexa de un convexo S en tiempo O(n log n), y este tiempo es óptimo.
Se puede calcular la envolvente convexa de una nube de puntos a partir de su diagrama de Voronoi en tiempo lineal, lo que junto al tiempo requerido para el cálculo del diagrama de Voronoi nos da un coste de O(n log n), que es el tiempo óptimo. Sin embargo, las constantes multiplicativas son tan grandes que el método no es práctico si no tenemos calculado de antemano el diagrama de Voronoi.
Algoritmo Quick Hull.
La idea del Quick Hull es ir descartando lo más pronto posible los puntos que no formarán parte de la frontera del cierre convexo, que suelen ser los más interiores de la nube de puntos.
Paso 1: Encontrar los cuatro puntos extremos de la nube de puntos (norte, sur, este y oeste) y formar un cuadrilátero con estos puntos como esquinas (aunque podría darse el caso de obtenerse sólo un triángulo e incluso una línea, lo cual no afecta el funcionamiento del algoritmo). Todos los puntos que hayan quedado dentro de este cuadrilátero no formarán ya parte de la frontera.
Paso 2: Los puntos exteriores al cuadrilátero se encontrarán divididos en cuatro (o menos) zonas no comunicadas.
En cada una de estas regiones obtendremos el punto más alejado al lado del cuadrilátero adyacente a dicha zona. De esta forma obtendremos una figura de hasta ocho vértices que descartará los puntos interiores como pertenecientes al borde del cierre convexo y dividirá los puntos exteriores en hasta ocho nuevas regiones.
Paso 3: Seguiremos actuando para cada nueva región según las reglas anteriores hasta que no queden vértices externos a la figura.
Esta figura resultante será el cierre convexo.
Teorema: El algoritmo Quick Hull calcula la envolvente convexa en tiempo O(n2).
(NOTA)
A pesar de ser de orden cuadrático, suele tardar menos tiempo que calculando el cierre convexo a través del diagrama de Voronoi.
Scan de Graham.
Este algoritmo utiliza una lista en la que va almacenando y ordenando correctamente los puntos que constituyen los extremos del cierre convexo.
Paso 1: Elegimos un primer punto (Por orden lexicográfico) para almacenar en la lista. A continuación vamos almacenando el resto en la lista, ordenados según el valor del ángulo que forman con el primer punto que escogimos.
Paso 2: Recorremos la lista que hemos formado, tomando en cada momento tres puntos: Inicial, Medio y Final.
Comprobamos si el ángulo que forman Inicial, Medio y Final (IMF) es negativo (sentido horario) o positivo (sentido antihorario).
Si es positivo, Medio pasará a ser Inicial, Final pasará a ser Medio y el siguiente elemento de la lista pasará a ser Final.
Si es negativo, Medio será borrado de la lista, Inicial pasará a ser Medio, el anterior elemento de la lista pasará a ser Inicial, y Final queda inalterado.
La lista obtenida al finalizar con todos los elementos de la lista será la frontera de la envolvente convexa de la nube de puntos.
Teorema: El Scan de Graham calcula la envolvente convexa en tiempo O(n log n), que es el tiempo óptimo.
Envolvimiento de regalo (Gift Wrapping).
Paso 1: Elegimos el punto A, que será el que menor coordenada y posea (así nos aseguramos que pertenezca al cierre convexo). Este punto será nuestro punto inicial.
Paso 2: Puede encontrarse otro punto B, que cumplirá que todos los puntos están situados a la izquierda de AB.
Paso 3: Similarmente, podemos encontrar C allí donde todos los puntos estén a la izquierda de BC. Repetimos este método para el resto de puntos.
La complejidad de este algoritmo será de nh, donde h es el número de caras del cierre convexo.
Algoritmo incremental.
La idea básica es ir añadiendo puntos mientras vamos modificando el cierre convexo.
Paso 1: Elegimos un punto. Si el nuevo punto está dentro del cierre, no hay nada que hacer. En otro caso, borramos todos los bordes que el polígono pueda ver, es decir, que se trazando una línea desde el punto no choquemos con ninguna otra.
Paso 2: Añadimos dos líneas para conectar el nuevo punto al resto del antiguo cierre.
Paso 3: Repetimos de nuevo desde el paso uno para los puntos que estén fuera del convex hull actual, hasta que todos los vértices estén dentro.
Si usamos una estructura para el cierre que nos permita coger una línea adyacente a otra en tiempo constante, podremos encontrar un lado visible en tiempo lineal y todos los demás en tiempo constante por lado. La actualización toma tiempo lineal.
El tiempo total es de O(n2).
Divide y vencerás.
Paso 1: Ordenamos los puntos según la coordenada x.
Paso 2: Dividimos los puntos en dos bloques, izquierda y derecha (L y R), de igual número de elementos, que cumplen que el punto más a la derecha de L está más a la izquierda que el punto más a la izquierda de R.
Paso 3: Recursivamente, encontramos el convex hull de L y R. Para mezclar el cierre de L y el de R es necesario unirlos utilizando las tangentes comunes más altas y bajas. La tangente superior común pude descubrirse en tiempo lineal explorando alrededor del cierre de L en el sentido de las agujas del reloj y en el cierre de R en el sentido antihorario. Para la tangente inferior giraremos en los sentidos inversos.
Las líneas que queden dentro de la envolvente que formamos al unir los cierres de L y R serán borradas.
Debido a que la mezcla no puede realizarse en tiempo lineal el cierre convexo puede ser encontrado en tiempo O(n log n).
APLICACIONES
Entre las múltiples aplicaciones existentes para el uso de la envolvente convexa, hablaremos de las dos siguientes: el cálculo del diámetro y el de la anchura de un conjunto.
Dada una nube de puntos S, el diámetro es la mayor distancia posible de entre todos los puntos de S.
La anchura es la menor longitud, de entre todas las posibles, entre dos rectas paralelas que contengan en su interior todos los puntos pertenecientes a S.
El uso de estas magnitudes va desde el cálculo de medidas de dispersión hasta el cálculo de trayectoria de robots.
El método más sencillo para calcular estas distancias es comparar todas las distancias para cada par de puntos y quedarnos con la apropiada. Pero el coste de este procedimiento es cuadrático.
Podemos mejorar este tiempo mediante el siguiente lema:
Lema: Tanto el diámetro como la anchura de S coinciden con el diámetro y la anchura de los puntos extremos de S.
De esta forma no es necesario comprobar todos los puntos, sino sólo los que estén en la frontera de S.
De todas formas, puede darse el caso extremo en el que todos los puntos pertenezcan al borde, siendo aún el coste de O(n2), por lo que mejoraremos el tiempo mediante otro método.
Definición: Un par antipodal vértice-vértice es una pareja de vértices extremos de S que tienen la propiedad de que un par de rectas paralelas que pasen sobre ellos contendrá a todos los puntos de S.
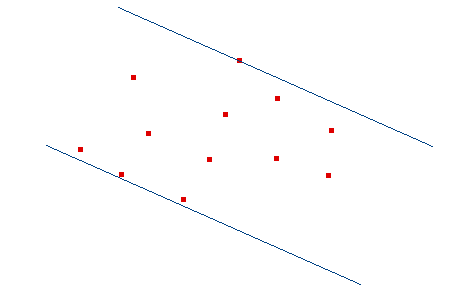
Definición: Un par antipodal vértice-arista son un vértice de S y una arista del cierre convexo que cumplen que la línea que contiene a la arista y su paralela que pase por el punto contienen a todos los puntos de S.
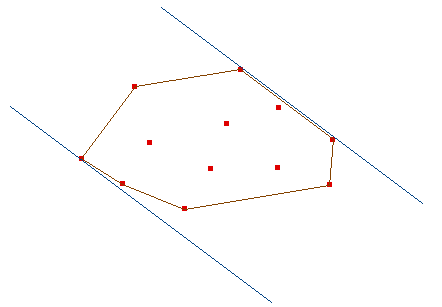
Lema: Si conocemos la envolvente convexa, podemos calcular todos los pares antipodales en tiempo lineal.
Demostración para pares vértice-arista:Teorema: Tanto el diámetro como la anchura de un conjunto S pueden ser calculados en tiempo lineal a partir del cierre convexo de S. Esto causa que el tiempo total sea de O(n log n).Partimos de una arista cualquiera, y hallamos el vértice que, junto con la arista, formen el triángulo de mayor área posible. De esta forma obtenemos un primer par antipodal en tiempo logarítmico (ya que la función de las áreas sólo dispone de un máximo).
El resto de los pares se averiguan de esta forma:
- Elegimos la siguiente arista en el sentido positivo.
- Comprobamos si el vértice actual es antipodal. Si no lo es probamos con el siguiente vértice (siguiendo el sentido positivo) hasta hallar el antipodal.
- Repetimos hasta tener todos los pares antipodales.
Puesto que nunca andamos en el sentido negativo, cada vértice sólo lo consideramos una vez y, por lo tanto, en tiempo lineal tendremos todos los pares antipodales.
Demostración para pares vértice-vértice:
Los vértices antipodales a un vértice v dado son todos aquellos comprendidos entre los vértices antipodales a las dos aristas incidentes en v. Luego podemos utilizar el método de la demostración anterior.
Demostración:Basta con comprobar que el diámetro es la mayor distancia entre pares antipodales vértice-vértice y que la anchura es la menor distancia entre pares antipodales vértice-arista.
BIBLIOGRAFÍA
- Hla Min and S. Q. Zheng, Time-Space Optimal Convex Hull Algorithms.
- A. M. DAY, The Implementation of an Algorithm to Find the Convex Hull of a Set of Three-Dimensional Points, ACM Transactions on Graphics, Vol. 9, No. 1, January 1990
Sección de ConvexHull de la página personal de Tim Lambert: https://www.cse.unsw.edu.au/~lambert/java/3d/ConvexHull.html
Profesor
Alberto Márquez
Autores de esta página
Francisco José Fernández Fadrique
Alberto García-Baquero Vega