Sección 1: Introducción

La envolvente convexa es una de las estructuras más ubicuas no sólo dentro de la Geometría Computacional, sino que expande sus ramas a otras disciplinas científicas y tecnológicas. En este tema nos centraremos, sobre todo en el cálculo de dicha estructura, aunque veremos también algunas de sus aplicaciones.

Sección 2: Definiciones y preliminares

Recordemos que un conjunto es convexo si dados dos puntos cualesquiera, el segmento que los une está contenido en el conjunto.  Una propiedad fundamental que se demuestra inmediatamente a partir de la definición es:

Lema 5.1: La intersección de conjuntos convexos es siempre un conjunto convexo.

Dado un conjunto finito de puntos en el plano P = {p₁,...,p_n} (con n mayor o igual que dos), definimos su envolvente convexa (o cierre convexo, convex hull en inglés) (denotada CH(P)) como el menor convexo que lo contiene. En este momento conviene aclarar varios puntos:

1. Evidentemente, la definición anterior podría extenderse a conjuntos no finitos, pero aquí el caso que nos interesa es el de conjuntos finitos.

2. Por abuso del lenguaje se designa muchas veces con el mismo nombre (envolvente convexa) tanto al menor convexo que contiene a un conjunto como a su frontera. Así a los puntos de la frontera los llamaremos extremos o vértices de la envolvente convexa.

3. Aunque existen convexos que no son polígonales, la envolvente convexa de una nube de puntos es siempre un polígono.

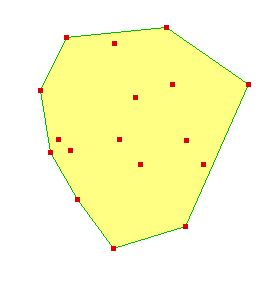
En la imagen se muestra un conjunto de puntos y su envolvente convexa. Con el mismo Applet de Java que ya usamos en el diagrama de Voronoi es posible construir la envolvente convexa de una nube de puntos en el plano (para usarlo basta con esperar a que se cargue el texto en el botón que está tras este párrafo y teclear con el ratón en él -con el ratón puedes añadir y mover puntos-).

Sorry, this WWW browser does not seem to understand Java applets.

Esto no es extraño porque como ya hemos señalado, es posible obtener la envolvente convexa a partir del diagrama de Voronoi.

Un par de  propiedades interesantes son:

Lema 5.2: La envolvente convexa de un conjunto P coincide con la intersección de todos los convexos que contienen al conjunto P.

Demostración: Lo demostramos por doble contención y denotamos por IC(P) a la intersección de todos los convexos que contienen a P. Por una parte, puesto que la envolvente convexa es un convexo, forma parte de la IC(P), luego IC(P) está incluido en CH(P). Pero por el Lema 5.1 la intersección de convexos es un convexo luego IC(P) es convexo y como contiene a P, está contenido en el menor convexo que contiene a P que es CH(P).         

Lema 5.3: Si p e CH(P) entonces p = a₁v₁+...+a_nv_k, donde v₁,...,v_n son los extremos de P y los a_i  son escalares que verifican dos condiciones:

1. a_i ≥ 0 

2. 1 = a₁+...+a_n

Sección 3: Algoritmos

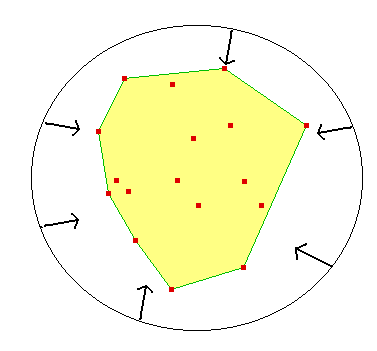
Con respectos a los algoritmos de cálculo de la envolvente convexa, ya hemos visto que es posible calcular la envolvente convexa de una nube de puntos a partir de su diagrama de Voronoi en tiempo lineal. Por lo tanto el tiempo total requerido es de O(n log n), que resulta ser óptimo. Sin embargo, las constantes involucradas suelen hacer este método no práctico salvo que tengamos calculado previamente el diagrama de Voronoi. Por lo tanto vamos a tratar de encontrar algún método más práctico. Algunos de estos métodos están basados en la idea intuitiva de que la envolvente convexa puede calcularse si suponemos que tenemos una banda elástica alrededor de los puntos y la soltamos, la envolvente convexa será la posición final que adopte dicha banda elástican (ver figura)

Aunque existen muchos algoritmos que calculan la envolvente convexa, aquí veremos sólo dos de ellos:

QuickHull

La idea básica del quickhull (envolvente rápida) es que para la mayoría de las configuraciones de puntos se puede en cada paso descartar muchos puntos a la hora de construir la envolvente convexa.

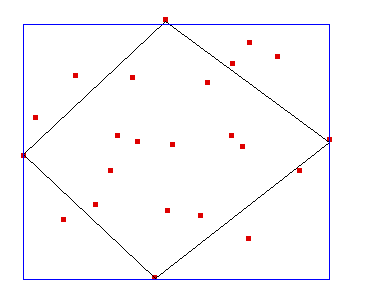
El primer paso del quickhull es encontrar los cuatro puntos extremos en las direcciones norte, sur, este y oeste y formar el cuadrilátero que ellos definen (este cuadrilátero puede ser degenerado), ahora todos los puntos en el interior de dicho cuadrilátero no son extremos, con lo cual pueden ser descartados. 

Así nos quedan puntos repartidos en cuatro regiones no conectadas entre si, trataremos cada una de estas regiones independientemente. En cada una de ellas encontramos el punto más alejado a la recta que define dicha región obteniendo así cuatro nuevos puntos y un polígono de a lo más ocho lados que divididirá a los puntos que no hemos eliminado en ocho regiones que tratamos individualmente siguiendo la misma regla anterior.

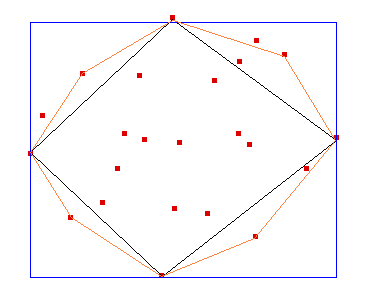
En nuestro ejemplo en el paso siguiente se obtine ya la envolvente convexa.

El QuickHull suele calcular la envolvente convexa en un tiempo mucho más corto que si lo hacemos a través del diagrma de Voronoi. Sin embargo, un análisis del algoritmo nos lleva a que su complejidad en tiempo es cuadrática. Por lo tanto, centrémosno ahora en encontrar un algoritmo óptimo.

Scan de Graham

El Scan de Graham construye una lista que al final será la de los puntos extremos ordenados. Supondremos que no existen tres puntos alineados (aunque esta condición puede ser eliminada). Comenzamos encontrando el primer punto con el orden lexicográfico, llamemosle p₀. A continuación ordenamos los puntos por el ángulo que forman con  p₀.

Suponemos que partimos de la lista ordenada así obtenida. En cada momento, tendremos tres puntos, llamémosles Inicial, Medio y Final. Nos preguntamos si el ángulo IMF es positivo (en el sentido contraro de las agujas del reloj o negativo. Si es positivo, la lista la dejamos como estaba y el anterior Medio pas a ser Inicial y el final pas a ser Medio y escogemos el siguiente en la lista para ser el nuevo Final. Si es negativo, eliminamos Medio de la lista, el anterior Inicial pasa a ser Medio, el Final sigue como Final y escogemos el anterior de la lista para ser el nuevo Incial. La lista resultante después de recorrer todos los puntos será la de los extremos de la envolvente convexa.

Teorema 5.1: El Scan de Graham calcula la envolvente convexa de n puntos en el plano en tiempo óptimo O(n log n).

Sección 4: Aplicaciones

Existe un gran número de aplicaciones de la envolvente convexa, pero citaremos aquí sólo dos: el cálculo del diámetro y el de la anchura de un conjunto.

Dada una nube de puntos S. El diámetro es la mayor distancia entre puntos de S y la anchura es la menor distancia entre dos rectas paralelas que contengan en su interior todos los puntos de S. Ambas cantidades tienen un uso muy variado como en robótica (trayectoria de robots) o como medidas de dispersión.

 Evidentemente, para calcular ambos parámetros se pueden diseñar algoritmos que funcionan en tiempo cuadrático (comprobar para cada par la distancia entre ellos y escoger la mayor de tales distancias como el diámetro). Se puede probar:

Lema 5.1: Tanto el diámetro como la anchura de S coinciden con el diámetro y la anchura de los puntos extremos de S.

Evidentemente aunque el Lema 5.1 permite mejorar el comportamiento de los algoritmos que habíamos comentado (puesto que no hay que probar entre todas las parejas de puntos sino sólo entre aquellos que están en la frontera de la envolvente convexa), aún podría darse el caso de que todos los puntos estuvieran en la frontera de la envolvente convexa y, por tanto, el tiempo aún con esta mejora seguiría siendo cuadrático. Para ver como podemos mejorar este tiempo necesitamos algunas definiciones: Un par de vértices de S se dicen antipodales si podemos trazar por ellos un par de rectas paralelas que contengan entre ellas a todo S. Evidentemente todo par antipodal es de vértices extremos.

Igualmente, dada una arista de la envolvente convexa de S y un vértice de dicho conjunto, se dicen antipodales si la recta prolongación del segmento y su paralela por el punto contienen al conjunto entre ellas.

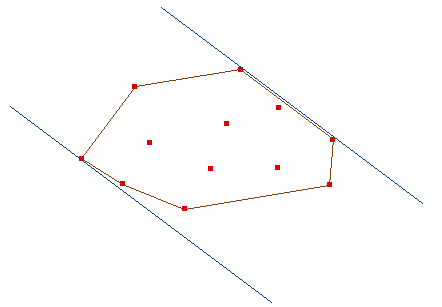
Lema 5.2: Todos los pares antipodales vértice-arista pueden ser calculados en tiempo lineal una vez conocida la envolvente convexa.

Demostración: Partiendo de una arista cualquiera, se encuentra el vértice tal que el área del triángulo que definen (el vértice y la arista) sea máximo

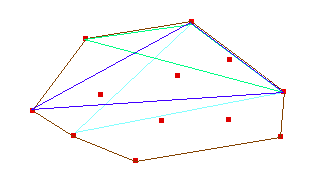
Ese será un primer par antipodal. Obsérvese que este cálculo puede hacerse en tiempo logarítmico porque la función de las áreas tiene un único máximo. El paso siguiente es considerar la siguiente arista en el sentido positivo y comprobamos con el mismo vértice, si no fuera antipodal, probaríamos con el siguiente en el sentido positivo y así hasta encontrar el antipodal. Puesto que nunca andamos en el sentido negativo, cada vértice sólo lo consideramos una vez y, por lo tanto, en tiempo lineal tendremos todos los pares antipodales.       

Corolario 5.1: Todos los pares antipodales vértice-vértice pueden ser calculados en tiempo lineal una vez conocida la envolvente convexa.

Demostración: Los vértices antipodales a un vértice v dado son todos aquellos comprendidos entre los vértices antipodales a las dos aristas incidentes en v. En la figura vemos un vértice  v (aquel marcado con una circunferencia negra) y sus dos aristas incidentes (azul y verde) y sus correspondientes vértices antipodales, los antipodales de v son todos aquellos marcados con un cuadrado.

Teorema 5.2: El diámetro y la anchura de un conjunto S puede ser calculado en timepo lineal a partir de la envolvente convexa de S (para un tiempo total de O(n log n).

Demostración: basta con comprobar que el diámetro es la mayor distancia entre pares antipodales vértice-vértice y que la anchura es la menor distancia entre pares antipodales vértice-arista.       

Problemas

1. Probar que dado un conjunto de puntos en el plano, se puede encontrar en tiempo O(n log n) un polígono simple que tenga a dicho conjunto como sus vértices.
2. Sea P un polígono monótono (existe una recta tal que toda perpendicular a dicha recta a lo más corta en dos puntos al polígono). Diseñar un algoritmo que calcule su envolvente convexa en tiempo lineal.
3. Dos conjuntos de puntos A y B se dicen que son linealmente separables si existe una recta r que los deja a cada uno en uno de los dos semiplanos que la recta define (a cada conjunto en un semiplano distinto).
   1. Demostrar que dos conjuntos son linealmente separables si y sólo si lo son sus envolventes.
   2. Demostrar que dos convexos son linealmente separables si y sólo si son disjuntos.
   3. Diseñar un algoritmo que decida cuando dos conjuntos son linealmente separables.
4. Probar que todo polígono convexo tiene cuatro vértices N, S, E, O (que pueden coincidir entre ellos) y cuatro cadenas monótonas entre ellos que son de N a W descendente hacia la izquierda, de W a S descendente hacia la derecha, de S a E ascendente hacia la derecha y de E a N ascendente hacia la izquierda.
5. Un polígono se dice ortogonal si todas sus aristas son horizontales o verticales. Y un polígono ortogonal se dice ortogonalmente convexo si el interior de cada línea horizontal o vertical en el polígono es un segmento.
   1. Encontrar una caracterización similar a la del problema 4 para polígonos ortogonales ortogonalmente convexos.
   2. Diseñar un algoritmo que decida cuando un polígono ortogonal es ortogonalmente convexo.
   3. Diseñar un algoritmo que encuentro el menor polígono ortogonalmente convexo que contiene a un polígono ortogonal dado.