El problema que tratamos en este tema es el de la localización de un punto en una subdivisión del plano. Aunque más adelante lo definiremos con más rigor, este problema puede ser descrito de la siguiente forma:
Supongamos que tenemos el plano subdividido en distintas regiones, dado un punto del plano, a cuál de las regiones pertenece.
Este problema tiene múltiples aplicaciones, algunas son sencillas de imaginar dado el enunciado anterior: tanto diseño asistido por ordenador (herramientas CAD-CAM), como navegación asistida pueden ser dos ejemplos, pero, en otros temas veremos otras aplicaciones más remotas como reconocedores automático de voz por ejemplo.
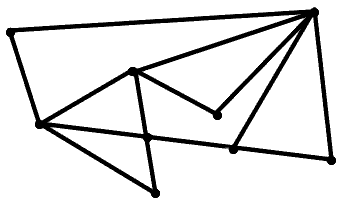
En todo lo que resta del tema, supondremos que tenemos una serie de vértices fijos en el plano unidos por segmentos rectilíneos que no se intersectan salvo en los vértices comunes tal y como muestra la figura.

Dicho esquema (inmersión de un grafo) al que llamaremos pslg y denotaremos por G divide el plano en regiones, por lo tanto, nuestro problema consistirá en: dado un nuevo punto, encontrar en cuál de las regiones de G está dicho punto.
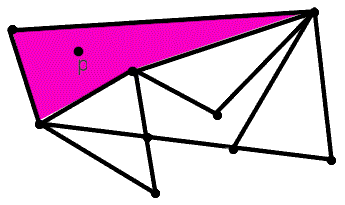
Así en la figura que aparece a continuación diremos que el punto p está en la región coloreada
Evidentemente, el caso más simple que se puede presentar es cuando los puntos y las aristas forman una línea poligonal cerrada. En dicho caso se tiene el siguiente
Teorema 2.1: Toda línea poligonal cerrada C divide el plano en dos regiones, una acotada y la otra no. Además, se puede determinar si un punto p está en la región acotada contando el número de veces que cualquier semirrecta que comienza en p atraviesa a C; p estará en dicha región si y sólo si dicho número es impar.
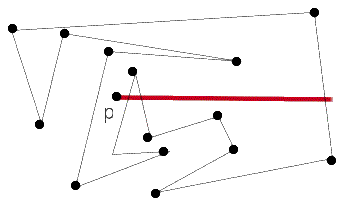
En la figura se observa que la semirrecta en rojo tiene tres intersecciones transversas con la curva, por tanto el punto p está en la región acotada.
El Teorema 2.1 es algoritmizable y es fácil ver que se puede desarrollar un algoritmo que siga su método y por tanto tenemos:
Corolario 2.1: Es posible determinar si un punto está en el interior de una región acotada por una línea poligonal simple cerrada en tiempo O(n).
La cuestión que queda pendiente es si el algoritmo al que nos acabamos de referir es óptimo o no. Para intentar responder a esta pregunta, primero nos formulamos un caso más simple y es cuando el polígono C es convexo (un polígono o un subconjunto cualquiera del plano es convexo si dados dos puntos cualesquiera en él, el segmento que los une también está incluido en el conjunto - se tratará en profundidad la convexidad cuando consideremos el tema de la envolvente convexa de una nube de puntos-). A continuación se muestra un algoritmo que resuelve dicho problema. Así, supongamos que tenemos un punto p y un polígono convexo C y queremos determinar si p está en el interior o el exterior de C
Este algorimo nos lleva a enunciar el siguiente
Teorema 2.2: Es posible determinar si un punto está en el interior de una región acotada por un poligono convexo en tiempo O(log n), con O(n log n) de preprocesamiento.
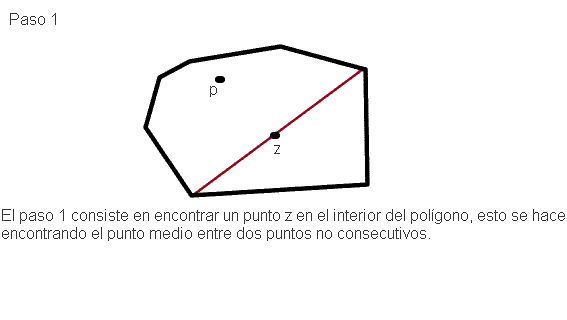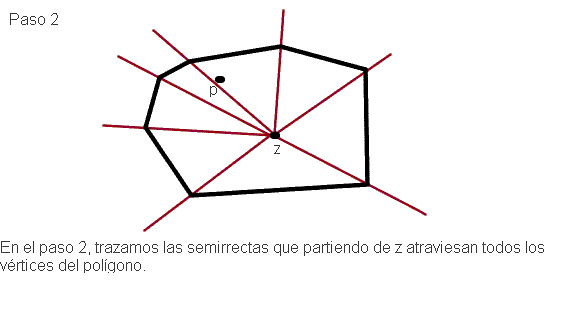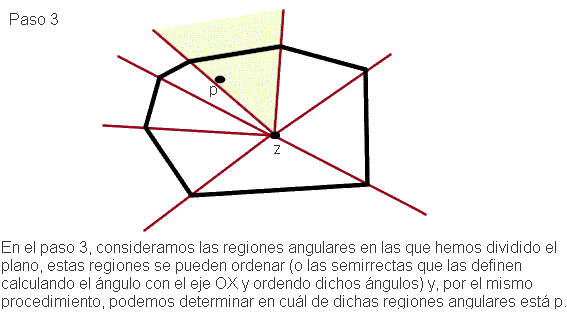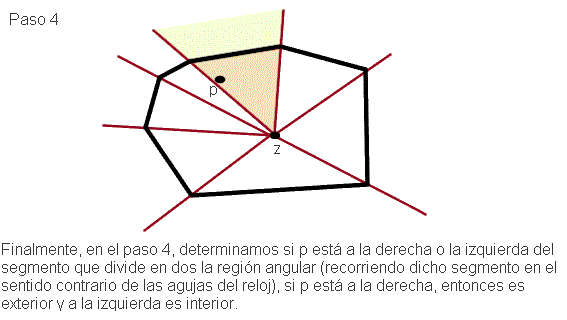
Demostración: El paso 1 del
algoritmo se puede realizar obviamente en tiempo constante. El paso 2 lleva un tiempo
lineal y el paso 3 (ordenar n números) se puede hacer en tiempo O(n log n), pero todos
estos pasos se pueden considerar como preprocesamiento y, por tanto, el único paso
significativo en el procesamiento es el 4, que dado que es la inclusión de un número en
una lista ordenada, se puede hacer en O(log n) como hemos anunciado.
![]()
En realidad, el algoritmo descrito anteriormente, puede ser aplicado no sólo a polígonos convexos, sino a una clase más amplia llamada polígonos estrellados. Un polígono se dice estrellado, si existe un punto z en su interior tal que todo segmento que une z con otro punto del interior del polígono está totalmente incluido en el polígono
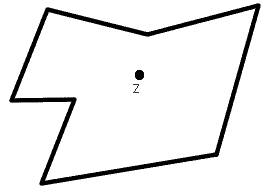
Obviamente, el punto z puede seguir jugando el mismo papel que desempeñaba en el algoritmo del Teorema 2.2 y, por tanto, el caso del polígono estrellado puede resolverse también en tiempo O(log n).
En esta sección veremos que, a pesar de que resolver el caso del test de inclusión en polígonos nos ha llevado un tiempo lineal, podremos resolver el problema general que habíamos planteado en la Sección 2 en tiempo logarítmico.
El método que vamos a dar se basa en la división en bandas, y entendemos por una banda a una región del plano de limitada por dos líneas horizontales y dividida por segmentos que no se cortan y que tienen ambos extremos en cada una de las dos horizontales
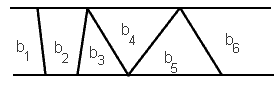
Obsérvese que una banda está dividida en regiones (dos infinitas y el resto trapecios o triángulos) y que se pueden ordenar dichas regiones de izquierda a derecha, o mejor dicho, se pueden ordenar los segmentos que atraviesan una banda. Esta propiedad, permite por tanto que dentro de una banda se pueda localizar un punto en tiempo logarítmico tal y como establece el siguiente
Lema 3.1: Se puede localizar un punto en una banda en tiempo O(log n) con O(n log n) de preprocesamiento.
Demostración: Como hemos dicho
anteriormente, basta con ordenar los segmentos de cada banda, puesto que no se cruzan
siempre es posible hacerlo y en tiempo O(n log n), para localizar un punto basta aplicar
un búsqueda binaria determinando en cada paso si el punto está a la derecha o a la
izquierda del segmento considerado, obviamente este paso puede ser realizado en tiempo
O(log n).
![]()
Así supongamos que tenemos una subdivisión del plano G y un punto p, el método funciona de la siguiente forma:
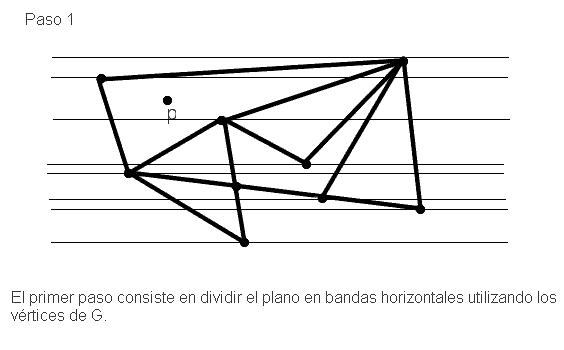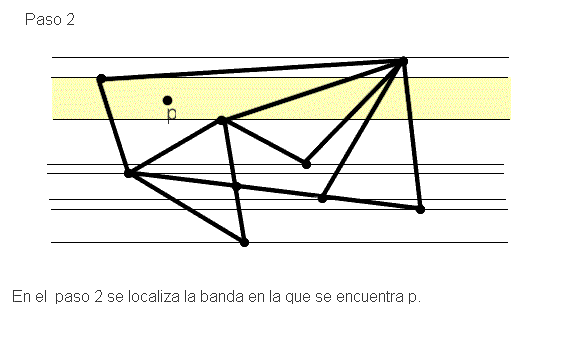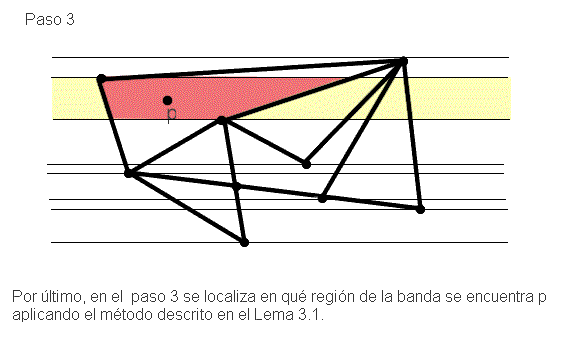
Por tanto podemos resolver el problema que nos planteamos en principio y enunciar
Teorema 3.1: Se puede localizar la región de un pslg G en la que está un punto en tiempo O(log n) con O(n2) de preprocesamiento.
Demostración: El paso 1 del método
descrito anteriormente se puede realizar en tiempo O(n log n) (O(n) para trazar las rectas
horizontales y O(n2) para determinar el orden en el que aparece cada segmento
en las bandas - para ello se utiliza la información de la banda anterior -). Este paso es
preprocesamiento y los dos pasos siguientes ya hemos visto que se pueden realizar cada uno
en O(log n) para un tiempo logarítmico en total
![]()