Los diagramas de Voronoi son una de las estructuras fundamentales dentro de la Geometría Computacional, de alguna forma ellos almacenan toda la información referente a la proximidad entre puntos. Son numerosísimas sus aplicaciones.
En este tema comenzaremos dando una idea intuitiva de lo que es un diagrama de Voronoi
plano para a continuación formalizar la definición y dar algunas propiedades básicas.
Para finalizar se mencionarán algunos algoritmos para su cálculo.
La idea del diagrama de Voronoi se basa
fundamentalmente en la proximidad. Suponemos dado un conjunto finito de puntos en el plano
P = {p1,...,pn} (con n mayor o igual que dos) y a cada pj
le asociamos aquellos puntos del plano que están más cerca o igual suya que de cualquier
otro de los pi con i distinto de j. Todo punto del plano queda así asociado a
algún pi, formándose conjuntos que recubren a éste. Existirán puntos que
disten lo mismo de dos elementos de P y que formarán la frontera de cada región. Los
conjuntos resultantes forman una teselación del plano, en el sentido de que son
exhaustivos (todo punto del plano pertenece a alguno de ellos) y mutuamente excluyentes
salvo en su
frontera. Llamamos a esta teselación Diagrama de Voronoi plano (denotado
Vor(P)). A cada una de las regiones resultantes las llamaremos regiones de
Voronoi o polígonos de Voronoi (denotado Vor(pi)). Los puntos
del conjunto reciben el nombre de generadores del diagrama.

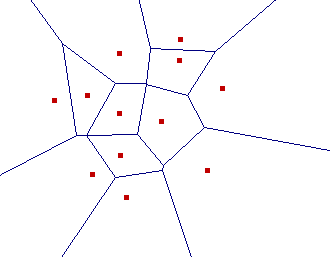
En la figura se muestra el diagrama de Voronoi de una nube puntos (en rojo) en el plano. Esta figura se ha obtenido mediante un Applet de Java (para usarlo basta con esperar a que se cargue el texto en el botón que está tras este párrafo y teclear con el ratón en él -con el ratón puedes añadir y mover puntos y además puedes determinar otras estructuras que se ven en este curso y de las que puedes encontrar referencias en estas páginas-)
Nótese que en la definición hemos usado una
desigualdad no estricta. Es también posible dar la definición a partir de la desigualdad
estricta, pero para nosotros las regiones de Voronoi serán cerrados. Al ser cada región
un cerrado contendrá a su frontera. Esta podrá estar formada por segmentos de recta,
semirrectas o rectas, que llamaremos bordes de la región.
Dentro de los bordes de una región distinguimos aquellos puntos que pertenecen a tres o
más regiones, que llamaremos vértices. Cuando un vértice pertenece a
cuatro o más regiones distintas diremos que el diagrama de Voronoi es degenerado.
Esto ocurre cuando los generadores correspondientes a cada una de las regiones en las que
se encuentra el vértice descansan sobre una misma circunferencia. Esta configuración es
muy inestable, en el sentido de que un pequeño cambio en la posición de cualquiera de
los estos generadores ocasiona la aparición de un nuevo borde con dos vértices en el
lugar donde estaba el vértice original. Los diagramas degenerados requieren en ocasiones
un tratamiento a parte que no resulta de importancia para el desarrollo de la exposición.
Para evitar esta dificultad en
adelante sólo consideraremos diagramas de Voronoi no degenerados.
Vamos a intentar encontrar un método que nos
permita un primer cálculo de los diagramas de Voronoi. Este primer método está basado
en que otra posible forma de aproximarnos a la definición de diagrama de Voronoi sería
considerando los semiplanos generados a partir de la bisectriz entre dos puntos
cualesquiera de P. Si denotamos por h(pi,pj) al semiplano que
contiene a pi de entre los dos generados por la bisectriz entre pi y
pj. Los puntos del
plano pertenecientes a h(pi,pj) son aquellos que están más
próximos a pi que a pj. Tomemos por comodidad p1 fijo y
consideramos la intersección de todos los h(p1,pj) con j mayor o
igual que 2. Cualquier punto perteneciente a dicha intersección estará más cerca de
p1 que de cualquier otro punto de P y por tanto dicha intersección
será la región de Voronoi de p1. Podemos enunciar dicha propiedad en el
siguiente
Lema 3.1: La intersección
de los semiplanos h(p1,pj) es Vor(p1).
A partir del Lema 3.1 podemos deducir que las regiones de Voronoi serán conjuntos
convexos al ser intersección de convexos (semiplanos). En la figura se ve el diagrama de
Voronoi que ya representamos anteriormente y una de sus regiones que se observa que es
convexo.

En las dos siguientes proposiciones veremos caracterizaciones para las regiones y bordes
no acotadas del diagrama.
Proposición 3.1: Una región de Voronoi es no acotada si y sólo si
su generador se encuentra en la frontera de la envolvente convexa.
Proposición 3.2: a) Los bordes de una región de Voronoi son rectas
infinitas
si y sólo si todos los puntos de P descansan sobre una misma recta.
b) El borde de Voronoi entre dos generadores es una semirrecta si y sólo si P
no es colineal y los generadores son consecutivos en la frontera de la envolvente convexa
de P.
c) El borde de Voronoi entre dos generadores es segmento de recta finito si y sólo
si P es no colineal y al menos uno de los dos generadores está en el interior de la
envolvente convexa de P.
Terminaremos esta sección con una caracterización de los bordes y vértices de un
diagrama de Voronoi. Hemos visto que los bordes son partes de bisectrices entre dos
generadores, y que los vértices son intersecciones de aquellas. Sin embargo, hay un
número cuadrático de bisectrices, mientras que la complejidad del diagrama es lineal.
Esto es, no todas las bisectrices definen un borde, ni todas las intersecciones son
vértices. Para caracterizar que bisectrices e intersecciones caracterizan los elementos
del diagrama daremos la siguiente definición:
Dado un punto q llamaremos círculo máximo vacío al mayor círculo centrado en
$q$ que no contiene a ningún generador del diagrama en su interior.
A partir de esta definición podemos dar una
caracterización de los
bordes y vértices de un diagrama de Voronoi.
Proposición 3.3: Dado un diagrama de Voronoi Vor(P) generado por un
conjunto de puntos P en el plano, se cumple:
a) Un punto q es vérticie de Vor(P) si y sólo si el círculo máximo vacío centrado en
q contiene tres o (en el caso de tratarse de un diagrama degenerado) más generadores en
su frontera.
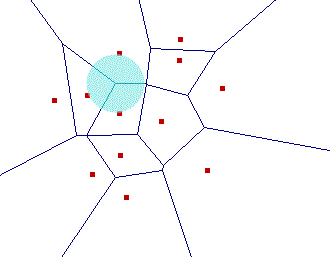
b) La bisectriz entre dos generadores define un borde de Vor(P) si y sólo si existe un
punto q sobre dicha bisectriz tal que el círculo máximo vacío centrado en q contiene
solamente a estos dos generadores en su frontera.

El gran número de aplicaciones del diagrama de Voronoi ha espoleado a numerosos
investigadores a desarrollar algoritmos para computarlo. Mencionaremos a continuación
cuatro de ellos sin detenernos en su desarrollo.
Tal y como hemos dicho anteriormente, podemos construir cada región de Voronoi por separado mediante la intersección de n-1 semiplanos. La construcción de n semiplanos puede construirse en tiempo O(n log n) mediante un algoritmo de divide y vencerás. Hacer esto para cada generador costaría un tiempo total de O(n2 log n).
Se basa en, supuesto construido el diagrama para k puntos, construir el diagrama para k+1. Este algoritmo emplea un tiempo de O(n) en la inserción de cada nuevo punto, con una complejidad total de O(n2). A pesar de su complejidad cuadrática, este ha sido el método más popular para construir el diagrama.
El diagrama de Voronoi puede construirse con un algoritmo tipo divide y vencerás en tiempo O(n log n). Esta complejidad es asintóticamente óptima, pero el algoritmo resulta bastante difícil de implementar.
Los pasos fundamentales del algoritmo
son:

Hasta mediados de los ochenta, la mayoría de
las implementaciones para computar el diagrama de Voronoi usaban el algoritmo incremental
cuadrático, admitiendo su mayor lentitud para evitar la complejidad del código divide y
vencerás. En 1985 Fortune inventó un inteligente algoritmo de barrido plano que resulta
tan simple como el incremental, pero en tiempo O(n log n).