Sección 1: Introducción.

Una de las principales herramientas en Geometría Computacional la consituyen las triangulaciones, tanto de nube de puntos como de polígonos. En este tema estudiaremos algunos de los aspectos más destacados de estas estructuras.

Una triangulación de una nube de puntos o de un polígono es una partición del dominio que definen (el cierre convexo en el caso de nube de puntos o el propio polígono en el otro caso) en triángulos.

Sección 2: Triangulaciones de nubes de puntos.

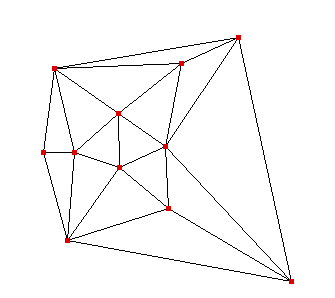
Como hemos definido en la Introducción, una triangulación de una nube de puntos es una partición del cierre convexo en triángulos. En la siguiente figura se puede ver una nube de puntos y una triangulación de su cierre convexo.

Tal y como se ha dicho en el Tema 4, el encontrar una triangulación de una nube de puntos viene determinado por un problema de interpolación, así allí nos planteábamos el siguiente problema:

P4-Topografía. Dadas las alturas sobre el nivel del mar de diversos puntos sobre los que se han efectuado mediciones precisas, querríamos deducir cual es la altura de un nuevo punto sin necesidad de efectuar nuevas mediciones. 

que quedaba modelizado mediante:

• Triangulación. Encontrar una triangulación que tenga a los puntos de S como vértices. Alguien podría decir que en este caso la traducción del P4 no es tan evidente, pero obsérvese que una vez conseguida dicha triangulación, a un punto le podemos suponer con mucha aproximación la altura proporcional de los vértices del triángulo en el que se encuentra (esta es la técnica llamada de interpolación lineal -que tiene muchísimas aplicaciones en campos muy diversos-). En realidad, se puede observar que para que esta técnica sea efectiva, los triángulos han de ser lo más equilátero posible. 

Así, en realidad lo que pretendemos es: entre todas las triangulaciones definidas sobre una nube de puntos, encontrar aquella tal que el menor ángulo definido sea máximo.

Si no se considerara la restricción que acabamos de introducir, se obtendrían triángulos como el señalado en rojo en la siguiente figura

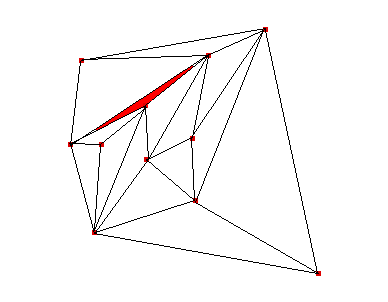
que evidentemente no sirven para el proceso de interpolación.

Hemos visto en el mismo tema que dicho problema puede ser resuelto mediante el diagrama de Voronoi, ya que su dual (la triangulación de Delaunay maximiza el mínimo ángulo) pero, en la práctica dichos métodos suelen ser muy costosos y de difícil implementación, así que aquí vamos a ver otros dos métodos que tienen como denominador común el uso del, así llamado, flip diagonal.

El flip diagonal consiste en dados dos triángulos que comparten una arista, si el cuadrilátero que definen es convexo, cambiar la arista común por la otra diagonal del cuadrilátero. Así en la triangulación "mala" de la nube de puntos que estamos considerando, escogemos los dos triángulos señalados

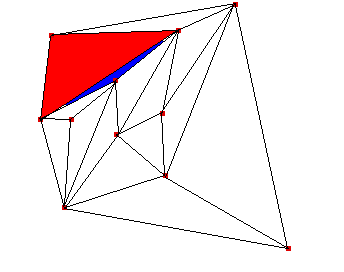
y, puesto que definen un cuadrilátero convexo, cambiamos la diagonal común para obtener otra triangulación:

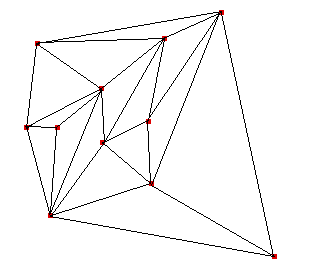
Obsérvese que en la nueva triangulación algunos de los ángulos "malos" han sido eliminados. En general, si un lado se puede cambiar y los ángulos obtenidos son mejores (el mínimo es más grande) se dice que el lado es ilegal. Se puede demostrar:

Teorema 4.1: Una triangulación es de Delaunay si y sólo si no tiene lados ilegales.

Así, en virtud del Teorema 4.1 podemos diseñar el siguiente algoritmo:

Paso 1. Construimos una triangulación cualquiera de la nube de puntos (esto se puede conseguir trazando tantos segmentos que no se corten como sea posible).
Paso 2. Mientras existan lados ilegales: hacemos flip sobre un lado ilegal.

Se puede probar que este procedimiento lleva siempre a la triangulación de Delaunay en tiempo O(n²) en el peor de los casos, pero, en general, este algoritmo se comporta mejor que si construimos el diagrama de Voronoi y después su dual.

El flip diagonal se puede aprovechar para diseñar otro algoritmo que, en la práctica funciona aún mejor, el llamado incremental aleatorio. En dicho método, se añaden tres puntos suficientemente alejados de los de la nube y se triangula (en este primer paso hay un solo triángulo), después se añaden los puntos uno a uno y cada punto se une con los tres vértices del triángulo al que pertenece, si en cada paso se ha creado algún lado ilegal, éste se corrige con flips.

Sección 3: Triangulaciones de polígonos

Una triangulación de un polígono es su subdivisión en triángulos mediante diagonales del polígono (que han de ser interiores. La primera cuestión que nos planteamos es si todo polígono admite una triangulación. Para resolver este problema neceitamos dos lemas previos:

Lema 4.1: Todo polígono tiene al menos un vértice convexo.

Demostración: El punto con menor coordenadas con el orden lexicográfico forzosamente ha de ser convexo.   

Lema 4.2: Todo polígono con más de cuatro vértices admite una diagonal.

Demostración: Sea v un vértice convexo y ab sus dos vértices adyacentes. Si ab es una diagonal ya hemos terminado, en caso contrario, ab ha de ser exterior al polígono o cortar a su borde, en cualquiera de los dos casos, el triángulo abv ha de contener vértices del polígono. Sea x el último vértice del polígono que nos encontramos al hacer un barrido con una recta paralela a ab en dirección a v.

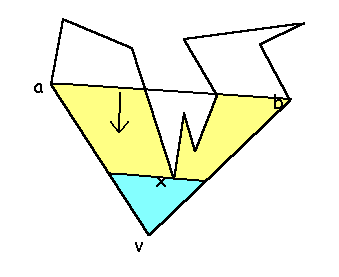
Como el triángulo que forma dicha recta cuando toca a x junto con v no puede contener ningún vértice del polígono, vx es una diagonal

Teorema 4.2: Todo polígono admite una triangulación.

Demostración: La demostración se realiza por inducción en el número n de vértices del polígono. Si n=3 ya hemos terminado. En caso contrario, por el Lema 4.2, el polígono admite una diagonal que lo divide en dos subpolígonos a los que se le puede aplicar la hipótesis de inducción.    

Si se quiere conseguir una triangulación con propiedades especiales (como maximir el mínimo ángulo), se pueden emplear técnicas similares a las vistas en el caso de triangulación de nubes de puntos. Veamos ahora algunas propiedades especiales que cumplen las triangulaciones:

Lema 4.3: Toda traingulación de un n-polígono tiene n-2 triángulos y utiliza n-3 diagonales.

Demostación: La demostración esa un sencillo ejercicio por inducción.

Lema 4.4: La suma de los ángulos internos de un n-polígono es (n-2)p.

Demostración: La suma de los ángulos internos del polígono es la suma de los ángulos internos de los triángulos de cualquier triangulación y por el Lema 4.3 esta es (n-2)p.       

Un concepto importante es el de dual de una triangulación (ya hemos visto que el dual del diagrma de Voronoi es la triangulación de Delaunay). Si tenemos una triangulación de un polígono, construimos su dual añadiendo un vértice en el interior de cada triángulo y unimos dos vértices si los triángulos que representan comparten una arista.

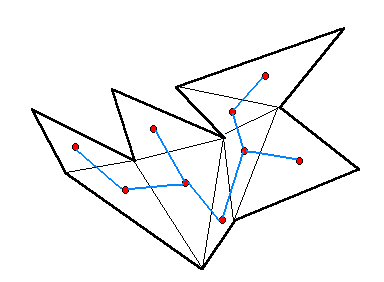
Es sencillo probar:

Proposición 4.1: El dual de una triangulación es un árbol de valencia máxima tres.

Ejercicios

1. ¿Cuál es la suma de los ángulos exteriores de un polígono?

2. Probar o dar un contraejemplo: todo árbol binario es el dual de la triangulación de un polígono.

3. Cuántas triangulaciones tiene el siguiente polígono:
   

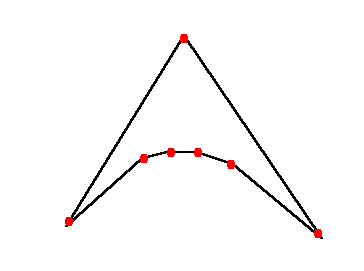
4. Probar que toda triangulación de un polígono tiene al menos dos orejas, donde una oreja es un triángulo que sólo comparte una arista con otro triángulo. ¿Ocurre lo mismo con triangulaciones de nubes de puntos?