Factorización
La noción clásica de divisibilidad se comporta de manera inesperada en presencia de divisores de cero. Aquí evitaremos estos problemas y estudiaremos la divisibilidad en dominios. Pondremos especial énfasis en el estudio de anillos donde sea posible generalizar el teorema fundamental de la aritmética. Este teorema, ya conocido para los números enteros, nos dice que todo número no nulo que no sea una unidad factoriza como producto de primos de manera esencialmente única. Este teorema también es conocido para el anillo de polinomios en una variable sobre un cuerpo, en cuyo caso los polinomios irreducibles juegan el papel de los enteros primos. Veremos además cómo este tipo de anillos es de utilidad a la hora de resolver ecuaciones diofánticas.
Divisores
Definición
En un dominio $R$, decimos que $a$ divide a $b$, o que $b$ es un múltiplo de $a$, y escribimos $a|b$, si $b=aq$ para cierto $q\in R$, que llamaremos cociente. Decimos que $a$ es un divisor propio de $b$ si además $a\neq 0$ y $a$ y $q$ no son unidades. Un elemento no nulo de $R$ es irreducible si no tiene divisores propios ni es una unidad. Dos elementos $a$ y $a^\prime$ son asociados si tanto $a| a^\prime$ como $a^\prime|a$.
El cero solo divide al cero, por tanto el cero es el único asociado del cero. Es más, si $a\neq 0$ y $a|b$ el cociente es único, es decir, solo hay un $q\in R$ tal que $b=qa$ pues si $b=q^{\prime}a$ entonces $qa=q^{\prime}a$ y por la propiedad cancelativa $q=q^\prime$.
Proposición
En un dominio $R$:
-
$a|b \Leftrightarrow (a)\supset (b)$.
-
$(a)=(a^\prime)\Leftrightarrow$ $a$ y $a^\prime$ son asociados $\Leftrightarrow a^\prime=ua$ para cierta unidad $u$.
-
$u$ es una unidad $\Leftrightarrow (u)=(1)$.
-
$a$ es un divisor propio de $b \Leftrightarrow (1)\supsetneq (a)\supsetneq (b)$.
Prueba
-
$(a)\supset (b)\Leftrightarrow (a)\ni b\Leftrightarrow a|b$.
-
La primera equivalencia se sigue del apartado anterior. Para la segunda, $\Leftarrow$ es obvio pues también $a=u^{-1}a^\prime$. Veamos $\Rightarrow$. Si $a$ y $a^\prime$ son asociados entonces $a^\prime=qa$ y $a=q^{\prime}a^\prime$, luego $a=q^{\prime}qa$. Si $a=0$ entonces $a^\prime=0$ y podemos tomar $u=1$. En caso contrario, por la propiedad cancelativa $1=q^{\prime}q$, luego $q^\prime$ y $q$ son unidades y podemos tomar $u=q$.
-
$\Rightarrow$ se ha visto antes. $\Leftarrow$ si $(u)=(1)$ entonces existe $r\in R$ tal que $ru=1$, con lo que $u$ es una unidad.
-
Es consecuencia de los tres apartados anteriores.
Si $a\in R$ no es una unidad, un divisor de $a$ es bien propio, bien asociado, o bien una unidad, pero no puede ser dos de estas cosas a la vez. En particular, si $a$ no es una unidad, $a^\prime$ es irreducible y $a|a^\prime$ entonces $a$ y $a^\prime$ son asociados. Los divisores de una unidad son las unidades. La primera caracterización de los asociados es especialmente interesante porque demuestra que cualquier propiedad de elementos de $R$ que pueda enunciarse en términos de sus correspondientes ideales principales es también válida para los elementos asociados.
Factorizaciones
En un dominio $R$, si $a\in R$ es un elemento no nulo que no es una unidad ni tampoco irreducible, entonces podemos descomponerlo como producto de dos divisores propios $a=bc$. Lo mismo podemos hacer con $b$ y con $c$, y así sucesivamente. Este procedimiento puede acabar en una descomposición de $a=b_1\cdots b_n$ como producto de elementos irreducibles $b_i\in R$, $1\leq i\leq n$, pero también podría no acabar nunca.
Definición
Una factorización de un elemento $a$ en un dominio $R$ es una descomposición de $a$ como producto de elementos irreducibles de $R$.
Para ver que en un dominio $R$ existen factorizaciones es útil el siguiente criterio.
Proposición
Sea $R$ un dominio en el que no existe una sucesión estrictamente creciente de ideales principales $(a_1)\subsetneq(a_2)\subsetneq(a_3)\subsetneq\cdots$ (o, equivalentemente, en el que toda sucesión creciente de ideales principales $(a_1)\subseteq(a_2)\subseteq(a_3)\subseteq\cdots$ es estacionaria). Entonces, todo elemento de $R$ no nulo que no sea una unidad tiene una factorización.
Prueba
Supongamos, por reducción al absurdo, que existe un elemento $a_1\in R$ no nulo que no es una unidad y no tiene factorización. En particular, $a_1$ no es irreducible (de lo contrario, el propio $a_1$ sería una factorización de $a_1$). Es decir, podemos descomponerlo como producto de divisores propios $a_1=a_2b_2$. Si $a_2$ y $b_2$ tuvieran una factorización, su producto sería una factorización de $a_1$, por lo que al menos uno de los dos no la tiene. Como el producto es conmutativo podemos suponer que es $a_2$ el que no la tiene. Por tanto, éste también se puede descomponer como producto de dos divisores propios $a_2=a_3b_3$ alguno de los cuales no tiene factorización. Una vez más podemos suponer que es $a_3$ y continuar indefinidamente con el proceso. Por construcción, esto nos da una sucesión creciente $(a_1)\subsetneq(a_2)\subsetneq(a_3)\subsetneq\cdots$ que es estricta porque todas las descomposiciones anteriores son como producto de dos divisores propios.
La condición del enunciado de la proposición anterior se suele denominar condición de cadena ascendente para ideales principales. Las condiciones de cadena juegan un papel muy importante en el álgebra moderna. Los anillos que satisfacen la condición de cadena ascendente para ideales cualesquiera se denominan noetherianos, por Emmy Noether. Los que cumplen la condición de cadena descendente para ideales arbitrarios se llaman artinianos, por Emil Artin, padre de Michael, el autor del libro que estamos siguiendo.
Definición
Un dominio de factorización única (también DFU o UFD) es un dominio donde todo elemento no nulo que no sea una unidad tiene una factorización en producto de irreducibles, y dos factorizaciones cualesquiera de un mismo elemento coinciden salvo orden y asociados, es decir, si
$$b_1\cdots b_s=c_1\cdots c_t$$
son productos de irreducibles, entonces $s=t$ y existe una permutación $\sigma\in S_s$ de $s$ elementos tal que $b_i$ y $c_{\sigma(i)}$ son asociados, $1\leq i\leq s$.
Un dominio con factorizaciones que no son únicas
En $\mathbb Z[\sqrt{-5}]\subset\mathbb C$,
$$9=3^2=(2+\sqrt{-5})(2-\sqrt{-5}).$$
Todo elemento de $\mathbb Z[\sqrt{-5}]$ es de la forma
$$z=a+b\sqrt{-5}=a+ib\sqrt{5}$$
donde $a,b\in\mathbb Z$. El cuadrado del módulo de tal elemento es
$$|z|^2=|a+b\sqrt{-5}|=a^2+5b^2\in\mathbb Z.$$
Como
$$|z_1z_2|^2=|z_1|^2\cdot|z_2|^2,$$
si $z\in \mathbb Z[\sqrt{-5}]$ es una unidad entonces $1=|z|^2\cdot|z^{-1}|^2$, así que $|z|^2\in\mathbb Z$ es invertible (y positivo), luego $|z|^2=1$. La única posibilidad de que esto ocurra es que $z=\pm 1$, por tanto las unidades de nuestro anillo son $\{\pm1\}$. Es más, las no unidades tienen módulo al cuadrado $>1$, así que si $z_1$ es un divisor propio de $z_2$ entonces $|z_1|^2<|z_2|^2$.
En $\mathbb Z[\sqrt{-5}]$ existen factorizaciones. En efecto, si hubiera una cadena $(z_1)\subsetneq(z_2)\subsetneq(z_3)\subsetneq\cdots$ entonces tendríamos que $|z_1|^2>|z_2|^2>|z_3|^2>\cdots\geq 0$, pero esto es imposible, no hay sucesiones infinitas estrictamente decrecientes de enteros no negativos.
Veamos que $3$ es irreducible. Si $3=z_1z_2$ es una factorización como producto de divisores propios entonces $3^2=|z_1|^2|z_2|^2$. No puede ser que $|z_i|^2=1$ ya que $z_i$ no es una unidad para ningún $i\in\{1,2\}$, luego, por el teorema fundamental de la aritmética para números enteros, $|z_1|^2=|z_2|^2=3$, pero no hay ningún elemento en $\mathbb Z[\sqrt{-5}]$ que tenga este cuadrado de módulo. Análogamente, $2\pm\sqrt{-5}$ es irreducible pues si $2\pm\sqrt{-5}=z_1z_2$ entonces de nuevo $|2\pm\sqrt{-5}|^2=3^2=|z_1|^2|z_2|^2$.
Por último, el $3$ no es un asociado de $2\pm\sqrt{-5}$ porque las únicas unidades de $\mathbb Z[\sqrt{-5}]$ son $\pm1$, luego las dos factorizaciones anteriores de $9$ como producto de irreducibles son esencialmente distintas.
Con el objetivo de caracterizar los DFU, introducimos un nuevo tipo de elemento.
Definición
Un elemento de un dominio $p\in R$ es primo si no es nulo ni una unidad y además si $p|ab$ entonces bien $p|a$ o bien $p|b$.
En términos de ideales, un elemento $p\in R$ no nulo es primo si y solo si $(p)\subset R$ es un ideal primo.
Proposición
En un dominio, todo elemento primo $p\in R$ es irreducible.
Prueba
El primo no es una unidad porque los ideales primos son distintos del total, $(p)\neq (1)$. Veamos que no tiene divisores propios. Para ello supongamos que $p=ab$ y demostremos que $a$ o $b$ es una unidad. Como $p|ab$, entonces $p|a$ o $p|b$. Si $p|a$ entonces $a=pq$, luego $p=ab=pqb$. Como los primos no son nulos y estamos en un dominio esto implica que $1=qb$, por tanto $b$ es una unidad. Si $p|b$ deducimos del mismo modo que $a$ tendría que ser una unidad.
Un irreducible que no es primo
Continuando con el ejemplo anterior, el irreducible $3\in \mathbb Z[\sqrt{-5}]$ no es primo porque $3|(2+\sqrt{-5})(2-\sqrt{-5})$ pero $3\nmid 2\pm \sqrt{-5}$ porque ambos son irreducibles pero no asociados.
Teorema
Sea $R$ un dominio en el que todo elemento no nulo que no sea unidad tiene una factorización. Entonces $R$ es un DFU si y solo si todo elemento irreducible de $R$ es primo.
Prueba
$\Rightarrow$ Sea $c\in R$ irreducible. Para ver que es primo, supongamos que $c|ab$. Hay que probar que $c|a$ o $c|b$. Como $c|ab$, entonces $ab=cd$ para cierto $d\in R$. Si $a=0$ entonces $c|a$ y si $b=0$, $c|b$. Si $a$ es una unidad, entonces despejando vemos que $c|b$, y si $b$ es una unidad $c|a$. Supongamos en adelante que $a$ y $b$ no son nulos ni unidades. Entonces $d$ no puede ser una unidad, ya que de lo contrario podriamos despejarla y $c=(d^{-1}a)b$ no sería irreducible, pues estaría descompuesto como producto de dos divisores propios. Por tanto $a$, $b$ y $d$ factorizan como productos de irreducibles,
$$\begin{array}{rcl}
a&=&a_1\cdots a_r,\cr
b&=&b_1\cdots b_s,\cr
d&=&d_1\cdots d_t.
\end{array}$$
Tenemos pues que
$$a_1\cdots a_rb_1\cdots b_s=cd_1\cdots d_t$$
son dos descomposiciones de un mismo elemento como producto de irreducibles. Por la unicidad, $c$ ha de ser asociado de algún $a_i$ o $b_j$, por tanto $c$ divide a $a$ o a $b$.
$\Leftarrow$ Veamos primero que si un primo $p$ divide a un producto de irreducibles $a_1\cdots a_r$ entonces $p$ es asociado de algún $a_i$. Procedemos por inducción en $r$. Para $r=1$, como $p|a_1$ y ambos elementos son irreducibles, han de ser asociados, según hemos visto anteriormente. Para $r>1$, como $p|a_1(a_2\cdots a_r)$, bien $p|a_1$ o bien $p|a_2\cdots a_r$. En el primer caso, ya tratado, $p$ es asociado de $a_1$, y en el segundo, por hipótesis de inducción, $p$ es asociado de algún otro $a_i$.
Consideramos ahora dos productos de irreducibles (primos) que son iguales
$$a_1\cdots a_r=b_1\cdots b_s.$$
Supongamos sin pérdida de generalidad que $1\leq r\leq s$. Procedemos por inducción en $r$. Si $r=1$ entonces $s=1$ puesto que un irreducible no tiene divisores propios. En este caso no hay nada que probar pues $a_1=b_1$. Sea $r>1$. Como $a_1|b_1\cdots b_s$ y $a_1$ es primo, $a_1$ es asociado de algún $b_i$, es decir $b_i=ua_1$ para cierta unidad $u\in R$. Por la propiedad cancelativa
$$a_2\cdots a_r=ub_1\cdots\widehat{b}_i\cdots b_s.$$
Observa que $b_1$ y $ub_1$ son asociados.
Por hipótesis de inducción, las últimas factorizaciones coinciden salvo orden y asociados, por tanto las anteriores también.
Proposición
En un DFU, un producto de irreducibles $a_1\cdots a_r$ divide a otro $b_1\cdots b_s$ si y solo si $r\leq s$ y, salvo reordenamiento, $a_i$ y $b_i$ son asociados $1\leq i\leq r$.
Prueba
Como el primer producto divide al segundo, existe $c\in R$ tal que $a_1\cdots a_rc=b_1\cdots b_s$. Si $c$ no es una unidad, lo factorizamos como producto de irreducibles $c=c_1\cdots c_t$,
$$a_1\cdots a_rc_1\cdots c_t=b_1\cdots b_s.$$
Por la unicidad de las factorizaciones, cada $a_i$ es asociado a un $b_j$ distinto, y salvo reordenamiento podemos suponer que son los $r$ primeros. Si $c$ fuera una unidad, la unicidad de las factorizaciones demostraría directamente que $r=s$ y que cada $a_i$ es asociado de un $b_j$ distinto.
En particular, en un DFU todo elemento tiene, salvo asociados, un número finito de divisores.
Corolario
Un DFU satisface la condición de cadena ascendente para ideales principales.
Prueba
Supongamos que existe una sucesión estrictamente creciente de ideales principales
$$(a_1)\subsetneq(a_2)\subsetneq(a_3)\subsetneq\cdots.$$
Entonces, los $a_i$ formarían una sucesión infinita de divisores no asociados de $a_1$.
Corolario
Dados dos elementos no nulos de un DFU, $a,b\in R$, existe un máximo común divisor $d\in R$, que es un elemento que satisface:
El máximo común divisor es único salvo asociados y se denota $\operatorname{mcd}(a,b)$ o $\gcd(a,b)$.
Prueba
Si $a$ o $b$ fuera una unidad, cualquier unidad sería un máximo común divisor puesto los divisores de una unidad son las unidades. En caso contrario, basta factorizar ambos elementos $a=a_1\cdots a_r$ y $b=b_1\cdots b_s$ como producto de primos y tomar $d$ como el producto del mayor subconjunto de los factores de $a$ que tienen asociados distintos entre los factores de $b$. La unicidad salvo asociados se deduce de que si $d$ y $d^\prime$ son máximos comunes divisores de $a$ y $b$ entonces por definición $d|d^\prime$ y $d^\prime|d$.
Si $a$ o $b$ es una unidad $\operatorname{mcd}(a,b)=1$. A diferencia de $\mathbb{Z}$ o $k[ x ]$, $k$ un cuerpo, en un DFU un máximo común divisor no tiene por qué satisfacer una identidad de Bézout, es decir, $\operatorname{mcd}(a,b)$ no tiene por qué estar en el ideal $(a,b)$. Veremos ejemplos más adelante.
Corolario
Dados dos elementos no nulos de un DFU, $a,b\in R$, existe un mínimo común múltiplo $m\in R$, que es un elemento que satisface:
El mínimo común múltiplo es único salvo asociados y se denota $\operatorname{mcm}(a,b)$ o $\operatorname{lcm}(a,b)$.
Prueba
Si $d$ es un máximo común divisor entonces $m=\frac{ab}{d}=a\frac{b}{d}=\frac{a}{d}b$ es un mínimo común múltiplo. En efecto, la primera propiedad es obvia. Comprobemos la segunda. Si $a|m^\prime$ y $b|m^\prime$ entonces $d|m^\prime$. Es más, $\frac{a}{d}|\frac{m^\prime}{d}$ y $\frac{b}{d}|\frac{m^\prime}{d}$. Como $\frac{a}{d}$ y $\frac{b}{d}$ no tienen factores primos asociados, su mínimo común múltiplo es el producto $\frac{ab}{d^2}$, así que $\frac{ab}{d^2}|\frac{m^\prime}{d}$. Multiplicando por $d$ deducimos que $m=\frac{ab}{d}|m^\prime$. La unicidad salvo asociados se deduce como en el caso del máximo común divisor.
Lema
Dada una sucesión creciente de ideales $I_1\subset I_2\subset I_3\subset\cdots$ en un anillo $R$, su unión $I_\infty=\cup_{n\geq 1}I_n$ es un ideal.
Prueba
Por un lado, $0\in I_1\subset I_{\infty}$. Por otro, dados $a,b\in I_\infty$ es obvio que $a,b\in I_n$ para cierto $n\geq 1$, por tanto $a+b$, $-a$ y $ra$, $r\in R$, pertenecen a $I_n\subset I_\infty$.
Prueba
Sea $R$ un DIP. Para probar que todo elemento no nulo que no sea unidad tiene una factorización, veamos por reducción al absurdo que no puede existir una sucesión estrictamente creciente de ideales principales
$$(a_1)\subsetneq(a_2)\subsetneq(a_3)\subsetneq\cdots.$$
Al estar en un DIP, $\cup_{n\geq 1}(a_n)=(b)$ para cierto $b\in R$. Como $b\in \cup_{n\geq 1}(a_n)$ este elemento ha de estar en cierto término de la sucesión, $b\in (a_n)$. Si esto es así $(b)\subset (a_n)\subsetneq (a_{n+1})\subset (b)$, lo cual es una contradicción.
Veamos ahora que todo irreducible $a\in R$ es primo. Probaremos por reducción al absurdo que el ideal $(a)$ es maximal y por tanto primo. Si $(a)$, que es un ideal propio y no trivial, no fuera maximal podríamos encontrar un ideal $I$ tal que $(a)\subsetneq I\subsetneq R$. Como $R$ es un DIP, $I=(b)$ para cierto $b\in I$. Entonces tenemos que $(a)\subsetneq(b)\subsetneq(1)$. Esto quiere decir que $b$ es un divisor propio de $a$, lo cual es una contradicción.
Más adelante veremos ejemplos de DFU que no son DIP.
Proposición
En un DIP, dados $a,b\in R$, cualquier $d\in R$ tal que $(a,b)=(d)$ es un $\operatorname{mcd}(a,b)$.
Prueba
Como $a,b\in (a,b)=(d)$, $d$ es un divisor común. Si $d^\prime|a$ y $d^\prime|b$ entonces $a,b\in (d^\prime)$, luego $(d)=(a,b)\subset (d^\prime)$ y por tanto $d^\prime|d$.
Acabamos de demostrar que en un DIP todo máximo común divisor satisface una identidad de Bézout.
Definición
Un dominio euclídeo es un dominio $R$ equipado con una función
$$\delta\colon R\setminus\{0\}\longrightarrow\{0,1,2\dots\},$$
llamada función de tamaño o euclídea, tal que dados $D,d\in R$ con $d\neq 0$, denominados dividendo y divisor, respectivamente, existen $c,r\in R$, cociente y resto, de modo que
$$D=dc+r$$
y bien $r=0$ o bien $\delta( r )<\delta(d)$. Esto se denomina división euclídea de $D$ por $d$.
Sabemos que $\mathbb Z$ y $k[ x ]$, con $k$ un cuerpo, son dominios euclídeos con función de tamaño el valor absoluto y el grado, respectivamente. En general, el cociente y el resto no están determinados de manera única por el dividendo y el divisor, por ejemplo
$$13=4\cdot 3+1=5\cdot 3+(-2).$$
Proposición
Un dominio euclídeo $R$ es un DIP. Es más, todo ideal no nulo de $R$ está generado por cualquiera de sus elementos no nulos de tamaño mínimo.
Prueba
Sea $I\subset R$ un ideal. Si $I=(0)$ ya es principal. Si no, tomamos $a\in I$, $a\neq 0$, de tamaño mínimo. Veamos que $I=(a)$.
Por un lado $(a)\subset I$ pues $a\in I$.
Por otro, dado $b\in I$ realizamos la división euclídea de $b$ por $a$,
$$b=ca+r.$$
El resto satisface $\delta(r)<\delta(a)$. Además $r=b-ca\in I$, por tanto $r=0$ y $b=ca\in (a)$.
Los enteros de Gauss
Vamos a ver que $\mathbb{Z}[i]$ con el cuadrado del módulo como función euclídea es un dominio euclídeo. Tomamos $D,d\in\mathbb{Z}[i]$, este último no nulo,$$\begin{array}{rcl}D&=&a+ib,\cr d&=& x+iy.\cr \end{array}$$
Encontrar un cociente euclídeo se reduce a hallar un múltiplo de $d$ en el interior del círculo de centro $D$ y radio $|d|$. Vamos a ver cómo hacerlo de manera analítica. Consideramos el número complejo
$$\frac{D}{d}=u+iv.$$
Aquí $u$ y $v$ son números reales, de hecho racionales, pero no necesariamente enteros. Aproximamos el anterior número complejo por un entero de Gauss
$$c=u_0+iv_0\in\mathbb Z[i]$$
de modo que sus partes real e imaginaria estén lo más cerca posible de las del complejo $\frac{D}{d}$,
$$\begin{array}{rcl} |u-u_0|&\leq &\frac{1}{2},\cr |v-v_0|&\leq &\frac{1}{2}. \end{array}$$
De este modo
$$\left|\frac{D}{d}-c\right|=\sqrt{(u-u_0)^2+(v-v_0)^2}\leq \frac{1}{\sqrt{2}}.$$
Veamos que $c$ es el cociente de una división euclídea. El resto sería $r=D-dc$ y su módulo es
$$|r|=|D-dc|=|d|\cdot \left|\frac{D}{d}-c\right|\leq \frac{|d|}{\sqrt{2}}<|d|.$$
Enteros cuadráticos
Un entero $n\in\mathbb Z$ es libre de cuadrados si no es divisible por el cuadrado de ningún primo, es decir, si entre sus factores primos no podemos encontrar dos asociados. Por ejemplo, $-4=2(-2)$ no es libre de cuadrados pero $6=2\cdot 3$ y $-1$ sí. Los cuerpos de números cuadráticos son $\mathbb Q[\sqrt{n}]\subset\mathbb C$ donde $n$ es un entero libre de cuadrados. Su anillo de enteros $R\subset\mathbb Q[\sqrt{n}]$ está formado por los elementos que son raíces de un polinomio mónico en $\mathbb Z[ x ]$. Se puede comprobar que $R=\mathbb Z[\sqrt{n}]$ si $n\equiv 2,3$ mod $4$ y $R=\mathbb Z[\frac{1+\sqrt{n}}{2}]$ si $n\equiv 1$ mod $4$. Decimos que $R$ es un anillo de enteros cuadráticos imaginarios si $n<0$. Los anillos de enteros cuadráticos imaginarios que son DIPs se obtienen para
$$n=−1, −2, −3, −7, −11, −19, −43, −67, −163.$$
De estos, son dominios euclídeos para
$$n=−1, −2, −3, −7, −11.$$
En todos estos casos podemos además tomar el cuadrado del módulo como función de tamaño. El resto de anillos de enteros cuadráticos imaginarios no son ni siquiera DFUs. Para $n>0$, obtenemos dominios euclídeos con la ’norma’ $N(a+b\sqrt{n})=a^2-b^2n$ para
$$n=2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57, 73.$$
Para $n=69$, $R=\mathbb Z[\frac{1+\sqrt{69}}{2}]$ es también un dominio euclídeo pero con una función de tamaño distinta de $N$.
Explora la posibilidad de realizar divisiones euclídeas en anillos de enteros cuadráticos imaginarios con la aplicación interactiva diseñada para ello.
Polinomios
En este epígrafe demostraremos que los anillos de polinomios con coeficientes en un DFU son también DFUs. En adelante $R$ denotará un DFU y $k=Q( R )$ su cuerpo de fracciones.
Definición
Un polinomio no nulo $f=f(x)=a_nx^n+\cdots+a_1x+a_0\in R[ x ]$ es primitivo si el máximo común divisor de sus coeficientes es $1$, es decir, si no existe ningún primo $p\in R$ tal que $p|a_i$ para todo $1\leq i\leq n$.
Los únicos polinomios constantes primitivos son las unidades de $R$.
Lema
Dado $f=f(x)=a_nx^n+\cdots+a_1x+a_0\in k[ x ]$ no nulo existe una constante $c\in k$, llamada contenido, y un polinomio primitivo $f_0(x)\in R[ x ]$ tal que
$$f(x)=c\cdot f_0(x).$$
Además $c$ y $f_0(x)$ son únicos salvo producto por unidades de $R$. Denotaremos $c=\operatorname{cont}(f)$.
Prueba
Veamos la existencia. Podemos quitar denominadores de los coeficientes de $f(x)$ multiplicando por una constante $d\in R$ no nula,
$$d\cdot f(x)\in R[ x ].$$
Si $e$ es el máximo común divisor de los coeficientes de $d\cdot f(x)$ vemos que podemos tomar
$$\begin{array}{rcl}
f_0&=&\frac{d}{e}\cdot f(x),\cr
c&=&\frac{e}{d}.
\end{array}$$
Probemos ahora la unicidad. Supongamos que $c\cdot f_0(x)=c^\prime\cdot f^\prime_0(x)$ siendo $f_0(x),f^\prime_0(x)\in R[ x ]$ primitivos. Podemos además suponer sin pérdida de generalidad que $c,c^\prime\in R$, multiplicando por un denominador común si fuera necesario. Como el máximo común divisor de los coeficientesde $f_0(x)$ es $1$, el máximo común divisor de los coeficientes de $c\cdot f_0(x)$ es $c$. Análogamente el máximo común divisor de los coeficientes de $c^\prime\cdot f^\prime_0(x)$ es $c^\prime$. Por la unicidad del máximo común divisor, $c$ y $c^\prime$ son asociados, es decir $c^\prime=u\cdot c$ donde $u\in R$ es una unidad. Por tanto, por la propiedad cancelativa, $f_0(x)=u\cdot f_0^\prime(x)$.
Si el contenido de un polinomio $f(x)\in k[ x ]$ está en $R$ entonces $f(x)\in R[ x ]$. Recíprocamente, el contenido de un polinomio $f(x)\in R[ x ]$ es el máximo común divisor de sus coeficientes, en particular $\operatorname{cont}(f)\in R$. Es más, dada una constante $a\in R$ tenemos que $a|f(x)$ si y solo si $a|\operatorname{cont}(f)$. Un polinomio $f(x)\in R[ x ]$ es primitivo si y solo si $\operatorname{cont}(f)=1$.
Teorema (Lema de Gauss)
El producto de polinomios primitivos en $R[ x ]$ es primitivo.
Prueba
Dado un primo $p\in R$, consideramos el homomorfismo de reducción módulo $p$
$$\phi_p\colon R[ x ]\longrightarrow (R/(p))[ x ]$$
definido en las constantes como $\phi_p(a)=\bar a$, $a\in R$, tal que $\phi_p(x)=x$. Es decir,
$$\phi_p(a_nx^n+\cdots+a_1x+a_0)=\bar a_nx^n+\cdots+\bar a_1x+\bar a_0.$$
El homomorfismo $\phi_p$ consiste simplemente en reducir los coeficientes módulo $(p)$. En particular $f\in \ker \phi_p$ si y solo si $p$ divide a todos los coeficientes de $f$. Por tanto $f\in R[ x ]$ es primitivo si y solo si $\phi_p(f)\neq 0$ para todo $p\in R$ primo. Si $f,g\in R[ x ]$ son primitivos entonces
$$\phi_p(f\cdot g)=\phi_p(f)\cdot \phi_p(g)\neq 0$$
para todo $p\in R$ primo ya que $(R/(p))[ x ]$ es un dominio. Es decir, $f\cdot g$ también es primitivo.
Corolario
Dados $f,g\in k[ x ]$ tenemos que $\operatorname{cont}(f\cdot g)=\operatorname{cont}(f)\cdot \operatorname{cont}(g)$.
Prueba
Tomamos $f,g\in k[ x ]$ y los descomponemos
$$\begin{array}{rcl} f&=&c\cdot f_0,\cr g&=&d\cdot g_0, \end{array}$$
con $c,d\in k$ y $f_0,g_0\in R[ x ]$ primitivos. Entonces
$$f\cdot g=(c\cdot d)\cdot (f_0\cdot g_0).$$
Como $f_0\cdot g_0$ es primitivo por el Lema de Gauss, esta es una descomposición válida del producto $f\cdot g$, así que $c\cdot d$ es su contenido.
Proposición
Dados $f,g\in R[ x ]$, si $g|f$ en $k[ x ]$ y $g$ es primitivo entonces $g|f$ en $R[ x ]$.
Prueba
Supongamos que $f=g\cdot q$ en $k[ x ]$. Como $g$ es primitivo,
$$\operatorname{cont}(f)=\operatorname{cont}(g)\operatorname{cont}(q)=\operatorname{cont}(q).$$
Como $f\in R[ x ]$ su contenido está en $R$, y como este coindice con el de $q$, entonces $q\in R[ x ]$, por lo que $g|f$ en $R[ x ]$.
Proposición
Un polinomio $f\in R[ x ]$ no constante es irreducible en $R[ x ]$ $\Leftrightarrow$ $f$ es primitivo e irreducible en $k[ x ]$.
Prueba
$\Leftarrow$ Supongamos por reducción al absurdo que $f$ no es irreducible en $R[ x ]$. Lo descomponemos como producto de divisores propios $f=gh$ en $R[ x ]$. Si $g$ fuera constante entonces dividiría al contenido de $f$, que es $1$, por tanto $g$ sería una unidad, lo cual entra en contradicción con que sea un divisor propio. Lo mismo ocurriría si $h$ fuera constante. Si $g$ y $h$ no son constantes entonces también son divisores propios de $f$ en $k[ x ]$, pues no podrían ser unidades, luego $f$ no sería irreducible.
$\Rightarrow$ Si $f$ no fuera primitivo tampoco sería irreducible en $R[ x ]$ pues su contenido sería un divisor propio. Supongamos por reducción al absurdo que $f$ tiene un divisor propio $g$ en $k[ x ]$. Aquí ser un divisor propio significa que $0<$ grado de $g<$ grado de $f$. Multiplicando por una constante no nula de $k$ si fuera necesario (por el inverso del contenido), podemos suponer que $g\in R[ x ]$ y es primitivo. Por la proposición anterior $g$ también divide a $f$ en $R[ x ]$ y por tanto es un divisor propio por cuestión de grados.
Una constante $a\in R$ es irreducible en $R[ x ]$ si y solo si lo es en $R$.
Prueba
Primero probaremos que todo elemento no nulo que no sea unidad de $R[ x ]$ tiene una factorización, usando el criterio de la condición de cadena ascendente para ideales principales. Supongamos por reducción al absurdo que tenemos una sucesión estrictamente creciente de ideales principales (que podemos suponer no nulos) en este anillo,
$$(f_1)\subsetneq (f_2)\subsetneq (f_3)\subsetneq\cdots.$$
Ningún $(f_n)$ puede ser el ideal total porque la sucesión estabilizaría necesariamente a partir de este punto. Por tanto, cada $f_{n+1}$ es un divisor propio de $f_{n}$, $n\geq 1$. En particular grado de $0\leq$ grado de $f_{n+1}\leq$ grado de $f_{n}$, es decir, los grados de los generadores forman una sucesion decreciente de enteros no negativos. Esta sucesión de enteros no nulos ha de estabilizar a partir de cierto punto, es decir, ha de existir cierto $n_0\geq 1$ tal que grado de $f_{n+1}=$ grado de $f_{n}$ para todo $n\geq n_0$, o equivalentemente $f_n=c_{n+1}f_{n+1}$ para cierto $c_{n+1}\in R$ que no puede ser una unidad ni tampoco nulo.
Si llamamos $d_n=\operatorname{cont}(f_n)$ tenemos que $d_n=c_{n+1}d_{n+1}$. Obtenemos así una sucesión estrictamente creciente de ideales principales en $R$:
$$(d_n)\subsetneq(d_{n+1})\subsetneq(d_{n+2})\subsetneq\cdots,$$
lo cual es imposible, ya que $R$ es un DFU y, por tanto, satisface la condición de cadena ascendente para ideales principales.
Veamos que todo elemento irreducible de $R[ x ]$ es primo. Consideraremos primero el caso en el que nuestro irreducible es un polinomio $f\in R[ x ]$ no constante. Supongamos que $f|gh$ en $R[ x ]$. Como $f$ también es irreducible en $k[ x ]$, que es un DFU, entonces $f$ es primo en $k[ x ]$ y por tanto $f|g$ o $f|h$ en $k[ x ]$. Los tres polinomios están en $R[ x ]$ y al ser $f$ irreducible en este anillo ha de ser primitivo, así que entonces $f|g$ o $f|h$ en $R[ x ]$.
Supongamos ahora que $a\in R\subset R[ x ]$ es una constante irreducible y que $a|gh$ en $R[ x ]$. Esto último equivale adecir que $a|\operatorname{cont}(gh)=\operatorname{cont}(g)\operatorname{cont}(h)$. Como $R$ es un DFU, el irreducible $a$ es primo en $R$, así que $a|\operatorname{cont}(f)$ o $a|\operatorname{cont}(g)$, es decir, $a|g$ o $a|h$.
Corolario
$R[x_1,\dots, x_n]$ es un DFU para todo $n\geq 0$.
El anillo $\mathbb Z[ x ]$
Este anillo es un DFU pero no es un DIP. Para comprobarlo basta ver que la identidad de Bézout para el máximo común divisor no siempre se da. Tanto $2$ como $x$ son primos en $\mathbb Z[ x ]$ según criterios vistos anteriormente. Como no son asociados, $\operatorname{mcd}(2,x)=1$, pero $1\notin (2,x)$ ya que todo elemento de este ideal es de la forma $2g+xh$ para ciertos $g,h\in \mathbb Z[ x ]$, así que su término independiente ha de ser par. Por tanto no hay una identidad de Bézout en este caso. El ideal $(2,x)\subset \mathbb Z[ x ]$ es de hecho un ejemplo de ideal que no es principal.
Tenemos que $R[ x ]\subset k[ x ]$. El siguiente resultado nos permite calcular cómo se ven los ideales del segundo dentro del primero.
Proposición
Si $(f)\subset k[ x ]$ es un ideal no nulo entonces $(f)\cap R[ x ]=(f_0)$, donde $f=c\cdot f_0$ con $c\in k$ el contenido y $f_0 \in R[ x ]$ primitivo.
Prueba
La intersección $(f)\cap R[ x ]$ es un ideal ya que es la imagen inversa de $(f)\subset k[ x ]$ a través de la inclusión $R[ x ]\hookrightarrow k[ x ]$. Veamos la igualdad de ideales por doble inclusión.
$\supset$ Como $f_0 \in R[ x ]$ y $f_0 =c^{-1}f \in (f)\subset k[ x ]$, tenemos que $f_0 \in (f)\cap R[ x ]$, lo cual demuestra esta inclusión.
$\subset$ Todo elemento $p \in (f)$ es de la forma $p =g\cdot f =(g \cdot c)\cdot f_0$. Si $p \in R[ x ]$, como $f_0 |p$ en $k[ x ]$ y $f_0$ es primitivo, $f_0 |p$ también en $R[ x ]$, así que $g \cdot c\in R[ x ]$ y por tanto $p \in (f_0)\subset R[ x ]$.
Finalmente veremos un par de condiciones suficientes más avanzadas para la irreducibilidad de un polinomio.
Teorema (Reducción módulo $p$)
Si $f=a_nx^n+\cdots+a_1x+a_0\in R[ x ]$ es un polinomio primitivo de grado $n>0$, $p\in R$ es un primo que no divide $a_n$ y la reducción de $f$ módulo $p$ es irreducible en $(R/(p))[ x ]$, entonces $f$ es irreducible en $R[ x ]$.
Prueba
Usaremos el homomorfismo $\phi_p\colon R[ x ]\rightarrow (R/(p))[ x ]$ de reducción módulo $p$ introducido en la demostración del Lema de Gauss. En general,
$$\operatorname{grado}(\phi_p(f))\leq \operatorname{grado}(f).$$
La condición sobre $a_n$ equivale a decir que concretamente para el polinomio $f$ del enunciado
$$\operatorname{grado}(\phi_p(f))= \operatorname{grado}(f).$$
Reduzcamos al absurdo. Si $f$ fuera reducible se descompondría como producto de dos divisores propios $f=gh$. Como $f$ es primitivo, ni $g$ ni $h$ puede ser constante, es decir
$$\operatorname{grado}(g),\operatorname{grado}(h)>0.$$
Al ser $\phi_p$ un homomorfismo,
$$\phi_p(f)=\phi_p(g)\phi_p(h).$$
Ninguna de las desigualdades
$$\begin{array}{rcl} \operatorname{grado}(\phi_p(g))&\leq &\operatorname{grado}(g),\cr \operatorname{grado}(\phi_p(h))&\leq &\operatorname{grado}(h), \end{array}$$
puede ser estricta ya que de ser así
$$\operatorname{grado}(\phi_p(f))=\operatorname{grado}(\phi_p(g))+\operatorname{grado}(\phi_p(h))<\operatorname{grado}(g)+\operatorname{grado}(h)=\operatorname{grado}(f),$$
pero $\operatorname{grado}(\phi_p(f))=\operatorname{grado}(f)$. Las dos igualdades de la ecuación anterior son ciertas porque tanto $R$ como $R/(p)$ son dominios, el segundo por ser $p$ primo. Por tanto,
$$\operatorname{grado}(\phi_p(g)),\operatorname{grado}(\phi_p(h))>0$$
y tanto $\phi_p(g)$ como $\phi_p(h)$ serían divisores propios de $\phi_p(f)$, que no sería irreducible.
Teorema (Criterio de Eisenstein)
Si $f=a_nx^n+\cdots+a_1x+a_0\in R[ x ]$ es un polinomio primitivo de grado $n>0$ y $p\in R$ es un primo tal que:
entonces $f$ es irreducible en $R[ x ]$.
Prueba
Esta demostración transcurre de manera exactamente igual que la anterior hasta la última frase, que no es válida en este caso. A partir de ahí continuamos del siguiente modo. Si $b_0, c_0\in R$ son los términos independientes de $g$ y $h$ entonces $a_0=b_0c_0$. Como $p|a_0$ y $p$ es primo, $p|b_0$ o $p|c_0$, pero no puede dividir a ambos a la vez ya que $p^2$ no divide a $a_0$. Esto prueba que bien $\phi_p(g)$ o bien $\phi_p(h)$ tiene término independiente no nulo. Por las condiciones del enunciado, $\phi_p(f)=\bar a_nx^n$ con $\bar a_n\neq 0$. Al ser $\phi_p(f)=\phi_p(g)\phi_p(h)$ un monomio y $R/(p)$ es un dominio, también $\phi_p(g)$ y $\phi_p(h)$ han de ser monomios. Como uno de ellos tiene término independiente no nulo, entonces ha de tener grado $0$, lo que contradice el cálculo al que se llega en la última ecuación de la demostración anterior.
Enteros de Gauss
Vamos a estudiar los primos y las factorizaciones en el anillo $\mathbb Z[i]$, que es un DFU y un DIP por ser un DE. En nuestros argumentos haremos uso de la conjugación compleja, del módulo y de su cuadrado. Recordemos que el cero es el único elemento de módulo cero y las unidades $\{\pm1,\pm i\}$ son los elementos de módulo $1$.
Proposición
Si $\pi\in\mathbb Z[i]$ es primo entonces su conjugado $\bar\pi$ también.
Prueba
Como la conjugación preserva productos, si $\bar\pi|ab$ entonces $\pi|\bar a\bar b$ luego $\pi|\bar a$ o $\pi|\bar b$, es decir $\bar\pi|a$ o $\bar\pi|b$.
Necesitaremos la siguiente observación sobre enteros primos.
Lema
Todo entero primo $p\in\mathbb Z$ satisface una y solo una de las siguientes ecuaciones:
-
$p\equiv 1$ mod $4$.
-
$p\equiv 3$ mod $4$.
-
$p=\pm2$.
Prueba
Si $p\equiv 0$ mod $4$ entonces $p$ sería un múltiplo de $4$, con lo cual no sería primo. Si $p\equiv 2$ mod $4$ entonces $p=2+4n=2(1+2n)$ para cierto $n\in\mathbb Z$, que solo es primo si $1+2n$ es invertible en $\mathbb Z$, es decir si y solo si $p=\pm2$.
Los primos 5, 13, 17, 29, 37, 41, 53, 61… son 1 mod 4, y 3, 7, 11, 19, 23, 31, 43, 47… son 3 mod 4.
Demuestra que hay una cantidad infinita de primos que satisfacen tanto la primera como la segunda ecuación.
Proposición
Si $\pi\in\mathbb Z[i]$ es tal que $|\pi|^2=p\in\mathbb Z$ es un entero primo entonces $\pi$ es primo en los enteros de Gauss y además bien $p=2$ o bien $p\equiv 1$ mod $4$.
Prueba
Supongamos que $\pi$ se descompone como $\pi=z_1z_2$ en $\mathbb Z[i]$. Entonces tenemos la ecuación $|z_1|^2|z_2|^2=|\pi|^2=p$ de números enteros. Como $p$ es primo en los enteros, necesariamente $|z_i|^2=1$ para algún $i\in\{1,2\}$, es decir, algún $z_i$ tendría que ser una unidad. Esto prueba que el entero de Gauss $\pi$ es irreducible, luego primo.
Veamos la ecuación en congruencias. Si $\pi=a+ib$ entonces $p=|\pi|^2=a^2+b^2$. En $\mathbb Z/4$ los únicos elementos que son cuadrados de otros son $0,1\in\mathbb Z$, por tanto $p=a^2+b^2$ puede ser $0$, $1$ o $2$ módulo $4$. La primera posibilidad queda descartada por el lema anterior y la tercera solo se da cuando $p=2$.
De este modo vemos que $1+i$, $2+i$, $3+2i$, $4+i$, $5+2i$, $6+i$, $5+4i$, $7+2i$, $6+5i$… son primos en los enteros de Gauss, así como sus conjugados y asociados. En particular $5=(2+i)(2-i)$ es una factorización como producto de primos en $\mathbb Z[i]$.
Proposición
Si $p\in\mathbb Z$ es un entero primo tal que $p\equiv 3$ mod $4$ entonces $p$ también es primo en los enteros de Gauss.
Prueba
Supongamos por reducción al absurdo que $p$ se descompone como producto de divisores propios $p=z_1z_2$, entonces tenemos la ecuación $p^2=|z_1|^2|z_2|^2$ en los enteros. Como ningún $z_i$ es una unidad, necesariamente $|z_1|^2=|z_2|^2=p$. Como $p\equiv 3$ mod $4$, esto es imposible por la proposición anterior.
Proposición
Salvo asociados, $1+i\in\mathbb Z[i]$ es el único primo cuyo módulo al cuadrado es $2$.
Prueba
Si $\pi=a+ib$ y $2=|\pi|^2=a^2+b^2$ es fácil observar que $a^2=b^2=1$, es decir $a=\pm1=b$. Esto nos da
$$\begin{array}{rcl}
1+i,&&\cr
1-i&=&(-i)(1+i),\cr
-1+i&=&i(1+i),\cr
-1-i&=&(-1)(1+i).
\end{array}$$
La factorización del $2$ como producto de primos en $\mathbb Z[i]$ es $2=(1+i)(1-i)$. Los dos primos que aparecen en esta factorización son asociados.
Veamos que para el resto de enteros primos $p\equiv 1$ mod $4$ también hay primos en los enteros de Gauss que lo tienen como módulo al cuadrado y que son de hecho los factores primos de $p$ en $\mathbb Z[i]$. Para ello necesitamos resultados técnicos sobre enteros primos.
Lema
Todo entero primo $p\in\mathbb Z$ no negativo satisface la ecuación $(p-1)!\equiv -1$ mod $p$.
Prueba
El resultado es obvio para $p=2$. Supongamos que $p>2$.
Observemos la definición del factorial
$$(p-1)!=1\underbrace{2\cdots (p-2)}(p-1).$$
Como $p$ es primo, $\mathbb Z/(p)$ es un cuerpo y todo elemento no nulo es una unidad. Ningún factor de la definición de $(p-1)!$ es divisible por $p$, porque es menor. Por tanto todos son unidades módulo $p$. En $\mathbb Z/(p)$ las únicas unidades que son inversas de sí mismas son $\pm 1$ ya que estas son las únicas raíces del polinomio $x^2-1=(x-1)(x+1)$. El primer factor de $(p-1)!$ es $1$ y el último es $p-1\equiv -1$ mod $p$, por tanto, todos los factores de en medio tienen una inversa diferente, que es otro elemento del mismo producto. Dicho de otro modo, el producto de los $p-3$ factores centrales se puede dividir en $(p-3)/2$ pares de elementos mutuamente inversos módulo $p$, con lo que este producto es congruente con $1$ módulo $p$, así que $(p-1)!\equiv 1(p-1)\equiv -1$ mod $p$.
Lema
Si $p\in\mathbb Z$ es un entero primo tal que $p\equiv 1$ mod $4$ entonces $p|(m^2+1)$ para cierto $m\in\mathbb Z$.
Prueba
Podemos suponer sin pérdida de generalidad que $p\geq 0$. Por el lema anterior, basta ver que $(p-1)!$ es un cuadrado módulo $p$. Como $p=4n+1$ entonces
$$\begin{array}{rcl}(p-1)!&=&1\cdot 2\cdots (4n-1)\cdot (4n)\cr &=& \underbrace{1\cdot 2\cdots (2n-1)\cdot (2n)}\cdot \underbrace{(2n+1)\cdot (2n+2)\cdots (4n-1)\cdot (4n)}.\end{array}$$
Para todo $1\leq i\leq 2n$, en $\mathbb Z/(p)$ el $i$-ésimo factor de la primera mitad es el opuesto por el signo del $i$-ésimo factor de la segunda mitad empezando por el final ya que ambos suman $4n+1=p\equiv 0$ mod $p$. Por tanto, módulo $p$,
$$\begin{array}{rcl}(p-1)!&\equiv& \underbrace{1\cdot 2\cdots (2n-1)\cdot (2n)}\cdot \underbrace{(-2n)\cdot (-2n-1)\cdots (-2)\cdot (-1)}\cr&\equiv&(-1)^{2n}\cdot 1^2\cdot 2^2\cdots (2n-1)^2 (2n)^2\cr &=&m^2\end{array}$$
para $m=(2n)!$.
En la demostración hemos visto que si $p=4n+1\geq 0$ podemos tomar $m=(2n)!$, pero este valor es innecesariamente alto. El siguiente resultado demuestra la existencia de otros más pequeños.
Lema
En las condiciones del lema anterior, siempre podemos tomar $\sqrt{p-1}\leq m\leq\frac{p}{2}$.
Prueba
Siempre hay un $0<m<p$ adecuado ya que simplemente se trata de resolver la ecuación $x^2+1\equiv 0$ mod $p$ y el lema anterior demuestra que hay solución. Es más, como la soluciones de esta ecuación no dependen del signo y $-x=p-x$ mod $p$, podemos escoger $0 < m\leq \frac{p}{2}$. Más aún, si $p|(m^2+1)$ entonces $p\leq m^2+1$, luego cualquier solución positiva satisface $m\geq \sqrt{p-1}$.
Para $p=13=4\cdot 3+1$, el valor del primer lema sería $m=(2\cdot 3)!=720$, pero el segundo lema nos garantiza que podemos tomar $3.46\dots=\sqrt{13-1}\leq m\leq\frac{13}{2}=6.5$, es decir $m=4,5$ o $6$. Probando estos tres posibles valores vemos que $m=5$ es el único que satisface $13|(5^2+1)=26$.
Proposición
Si $p\in\mathbb Z$ es un entero primo tal que $p\equiv 1$ mod $4$ entonces $p$ no es primo en los enteros de Gauss.
Prueba
Sabemos que $p|(m^2+1)$ para cierto $m\in\mathbb Z$, es decir $p|(m+i)(m-i)$ pero $p$ no divide a $m\pm i$ ya que no divide a su parte imaginaria. Por tanto $p$ no es primo en $\mathbb Z[i]$.
Teorema
Si $p\in\mathbb Z$ es un entero primo tal que $p\equiv 1$ mod $4$ entonces, salvo asociados, hay exactamente dos primos en los enteros de Gauss cuyo módulo al cuadrado es $p$. Además estos dos primos son conjugados $\pi,\bar\pi\in\mathbb Z[i]$.
Prueba
Como $p$ no es primo en $\mathbb Z[i]$ podemos descomponerlo como producto de dos divisores propios $p=z_1z_2$. Tenemos la ecuación $p^2=|z_1|^2|z_2|^2$ en los enteros. Como ningún $z_i$ es una unidad, necesariamente $|z_1|^2=|z_2|^2=p$. Según hemos visto antes estos $z_i$ son primos en $\mathbb Z[i]$. Es más $z_1\bar z_1=|z_1|^2=p=z_1z_2$, por tanto $z_2=\bar z_1$.
Llamemos $\pi=z_1=a+ib$. Veamos que $\pi$ y $\bar\pi$ no son asociados. Los asociados de $\pi$ son
$$\begin{array}{rcl}
a+ib,&&\cr
(-1)(a+ib)&=&-a-ib,\cr
i(a+ib)&=&-b+ia,\cr
(-i)(a+ib)&=&b-ia.
\end{array}$$
Veamos que ninguno de estos enteros de Gauss puede ser $\bar\pi=a-ib$. Si fuera el primero tendríamos que $b=0$, pero entonces $p=|\pi|^2=a^2$, lo cual es una contradicción. Si fuera el segundo tendríamos que $a=0$ y llegaríamos a la contradicción $p=|\pi|^2=b^2$. Si fuera el tercero tendríamos que $a=-b$, con lo que $\pi=a(1-i)$, que solo es primo si $a$ es una unidad, pero en este caso $p=|\pi|^2=2\not\equiv 1$ mod $4$. Análogamente si fuera el último tendríamos que $a=b$ y $\pi=a(1+i)$, incurriendo en la misma contradicción que en el caso anterior.
Finalmente, comprobemos no puede haber más que estos primos de Gauss y sus asociados con módulo al cuadrado $p$. En efecto, si $\pi^\prime\in\mathbb Z[i]$ satisficiera $p=|\pi^\prime|^2=\pi^\prime\bar\pi^\prime$ entonces como $\pi^\prime|p=\pi\bar\pi$ tendríamos que bien $\pi^\prime|\pi$ o bien $\pi^\prime|\bar\pi$, es decir, como estos tres elementos son primos, $\pi^\prime$ es asociado a $\pi$ o a $\bar\pi$.
En las condiciones del enunciado anterior, la factorización de $p$ en $\mathbb Z[i]$ es $p=\pi\bar\pi$. Para $p=5$ los dos primos de Gauss son $\pi=2+i$ y $\bar\pi=2-i$. Los asociados de $\pi$ son $2+i$, $-2-i$, $-1+2i$ y $1-2i$. Los asociados de $\bar\pi$ son los conjugados de los anteriores, $2-i$, $-2+i$, $-1-2i$ y $1+2i$.
Factores de $p\equiv 1$ mod $4$
Dado un entero primo $p\in\mathbb Z$ tal que $p\equiv 1$ mod $4$, podemos hallar su factorización como producto de primos $p=\pi\bar\pi$ en $\mathbb Z[i]$ del siguiente modo. Primero encontramos un $m\in\mathbb Z$ tal que $p|(m^2+1)$. Hemos visto en una demostración anterior que $p$ no divide a $m\pm i$, pero $\pi|p$ y $p|(m^2+1)=(m+i)(m-i)$, por tanto el primo de Gauss $\pi$ divide a $m+i$ o a su conjugado, y análogamente $\bar\pi$. Deducimos que $\pi$ y $\bar \pi$ son $\operatorname{mcd}(p,m+i)$ y $\operatorname{mcd}(p,m-i)$.
Por ejemplo, para $p=13$ hemos visto que podemos tomar $m=5$. Calculamos $\operatorname{mcd}(13, 5+i)$, mediante el algoritmo de Euclides. Como el módulo de $13$ es mayor que el de $5+i$, comenzamos realizando la división euclídea del primero por el segundo,
$$13=(5+i)\cdot 3+(-2-3i).$$
Ahora dividimos $5+i$ por el resto de la anterior división,
$$(5+i)=(-2-3i)(-1+i)+0.$$
El resto de esta división es $0$. El máximo común divisor es el último resto no nulo,
$$\pi=-2-3i.$$
Hasta el momento hemos conseguido factorizar los primos enteros en $\mathbb{Z}[i]$ y por tanto calcular aquellos primos de Gauss que son factores de un primo entero. Veamos que estos son todos los primos de Gauss posibles y que por tanto hemos dado ya una descripción completa de todos los primos en $\mathbb Z[i]$.
Proposición
Todo primo en $\mathbb Z[i]$ divide a un primo en $\mathbb Z$.
Prueba
Sea $\pi\in\mathbb Z[i]$ un primo. Factorizamos $|\pi|^2\in\mathbb Z$ como producto de primos enteros $|\pi|^2=p_1\cdots p_n$. Como $|\pi|^2=\pi\bar\pi$ entonces $\pi|p_1\cdots p_n$ así que $\pi|p_i$ para cierto $1\leq i\leq n$.
Recapitulando, los primos de Gauss son los siguientes, salvo asociados:
-
$1+i$.
-
Los primos enteros $p\in \mathbb{Z}$, $p > 0$, tales que $p\equiv 3$ mod $4$.
-
Para cada primo entero $p\in\mathbb{Z}$, $p > 0$, tal que $p\equiv 1$ mod $4$, dos primos de Gauss conjugados $\pi$ y $\bar{\pi}$ tales que $p=\pi\bar{\pi}$, cuyo cálculo se ha explicado en un ejemplo anterior.
Hay una cantidad infinita de primos de Gauss tanto del segundo tipo como del tercer tipo.
En $\mathbb{Z}[i]$, los asociados de un elemento se obtienen multiplicándolo por las unidades $\{\pm1,\pm i\}$.
Factorizar un entero en $\mathbb Z[i]$
Para factorizar $n\in\mathbb{Z}$, $n\neq 0,\pm1$, como producto de primos en $\mathbb{Z}[i]$, primero lo factorizamos como producto de primos en $\mathbb{Z}$, $n=p_1\cdots p_r$, y luego factorizamos cada $p_i\in\mathbb{Z}$ como producto de primos en $\mathbb{Z}[i]$. Recuerda que si $p_i\equiv 3$ mod $4$ entonces ya es primo de Gauss, la factorización del $2$ como producto de primos de Gauss es $2=(1+i)(1-i)$, y el caso $p_i\equiv 1$ mod $4$ se ha tratado más arriba. Por ejemplo,
$$
\begin{array}{rcl}
n&=&1350\cr
&=&2\cdot 3^3\cdot 5^2\cr
&=&(1+i)\cdot(1-i)\cdot 3^3\cdot(2+i)^2\cdot(2-i)^2.
\end{array}
$$
Definición
Diremos que un entero de Gauss $z=a+ib$ no tiene primitivo si $z\neq 0$ y $\operatorname{mcd}(a,b)=1$.
Un entero de Gauss no nulo es primitivo si y solo no es divisible por ningún entero distinto de $\pm1$.
Lema
Sea $z$ un entero de Gauss primitivo y $\pi$ un primo de Gauss tal que $|\pi|^2=p$ es un entero primo $p\equiv 1$ mod $4$. Si $\pi|z$ entonces $\bar{\pi}\nmid z$.
Prueba
Por reducción al absurdo, si también $\bar{\pi}\mid z$ entonces $\operatorname{mcm}(\pi,\bar{\pi})|z$. Como $\pi$ y $\bar{\pi}$ son primos no asociados, $\operatorname{mcm}(\pi,\bar{\pi})=\pi\bar{\pi}=p$, por tanto $p|z$ y $z$ no sería primitivo.
Factorización de enteros de Gauss primitivos
Sea $z\in\mathbb{Z}[i]$ primitivo. Supongamos que $z=\pi_1\cdots\pi_r$ es su factorización como producto de primos de Gauss. Como $z$ es primitivo, ningún $\pi_i$ es un primo entero $p\equiv 3$ mod $4$, así que $|\pi_i|^2=2$, y en dicho caso $\pi_i$ es asociado de $1+i$, o bien $|\pi_i|^2=p$ es un primo entero $p\equiv 1$ mod $4$. Es más, en este último caso ni $\bar{\pi}_i$ ni ninguno de sus asociados puede aparecer en la factorización.
Por tanto, para factorizar $z$ en $\mathbb{Z}[i]$ podemos proceder del siguiente modo. Primero, factorizamos $|z|^2$ como producto de potencias de primos enteros positivos,
$$|z|^2 = p_1^{n_1}\cdots p_s^{n_s}.$$
Entonces
$$z=u\pi_1^{n_1}\cdots \pi_s^{n_s}$$
donde:
-
Si $p_i=2$ entonces $\pi_i=1+i$.
-
Si $p_i\equiv 1$ mod $4$, entonces $\pi_i|p$. Para calcularlo, factorizamos $p_i$ como producto de primos de Gauss, $p_i=\pi\bar{\pi}$, según el ejemplo anterior y dividimos $\frac{z}{\pi}$ en $\mathbb{C}$. Si $\frac{z}{\pi}$ resulta ser un entero de Gauss entonces $\pi_i=\pi$, y si no $\pi_i=\bar{\pi}$.
-
$u$ es una unidad, $u\in\{\pm1,\pm i\}$, que se determina a posteriori.
Veámoslo en el caso particular $z=201-43i$. En este caso
$$|z|^2=201^2+43^2=42250=2\cdot 5^3 \cdot 13^2.$$
Las factorizaciones de $5$ y de $13$ en $\mathbb{Z}[i]$ son $5=(2+i)(2-i)$ y $13=(3+2i)(3-2i)$, por tanto
$$z=u(1+i)(2\pm i)^3(3\pm 2i)^2.$$
Para determinar qué factor del $5$ aparece realmente, dividimos $z$ por uno de ellos en $\mathbb{C}$, por ejemplo
$$
\begin{array}{rcl}
\frac{z}{2+i}&=&\frac{(201-43i)(2-i)}{(2+i)(2-i)}\cr
&=&\frac{359}{5}-\frac{287}{5}i.
\end{array}
$$
Como no es un entero de Gauss, $2+i\nmid z$, así que $2-i\mid z$, luego
$$z=u(1+i)(2-i)^3(3\pm 2i)^2.$$
Ahora, para hallar qué factor del $13$ aparece realmente, dividimos $z$ por uno de ellos en $\mathbb{C}$,
$$
\begin{array}{rcl}
\frac{z}{3-2i}&=&\frac{(201-43i)(3+2i)}{(3-2i)(3+2i)}\cr
&=&23+21i.
\end{array}
$$
Este sí es un entero de Gauss, por tanto $3-2i\mid z$ y
$$z=u(1+i)(2-i)^3(3- 2i)^2.$$
Para hallar la unidad, calculamos el producto de la derecha
$$(1+i)(2-i)^3(3- 2i)^2=-43-201i,$$
así que $u=i$,
$$z=i(1+i)(2-i)^3(3-2i)^2.$$
La unidad $i$ se puede incorporar a cualquier factor primo, por ejemplo al primero, $i(1+i)=-1+i$, y en conclusión
$$z=(-1+i)(2-i)^3(3-2i)^2$$
es una factorización de $z$ como producto de primos de Gauss.
Factorización en $\mathbb Z[i]$
En general, todo entero de Gauss $z=a+ib\in\mathbb{Z}[i]$ se puede descomponer como $z=n\cdot z^\prime$, con $n=\operatorname{mcd}(a,b)$ y $z^\prime\in\mathbb{Z}[i]$ primitivo. La factorización de $z$ como producto de primos de Gauss se obtiene multiplicando las correspondientes factorizaciones de $n$ y $z^\prime$, que se realizan según indicamos aquí y aquí.
Por ejemplo, $z=15+45i=15(1+3i)$. Por un lado $n=15=3\cdot 5=3\cdot(2+i)\cdot (2-i)$. Por otro lado $z^\prime=1+3i$, $|z^\prime|^2=1^2+3^2=10=2\cdot 5$. Por tanto
$$z^\prime=u(1+i)(2\pm i).$$
Para saber qué factor de $5=(2+i)\cdot (2-i)$ divide a $z^\prime$ realizamos la siguiente operación en $\mathbb{C}$,
$$
\begin{array}{rcl}
\frac{1+3i}{2+i}&=&\frac{(1+3i)(2-i)}{(2+i)(2-i)}\cr
&=&1+i.
\end{array}
$$
Por tanto
$$z^\prime=u(1+i)(2+ i).$$
De hecho, el cálculo anterior nos demuestra que la unidad es $u=1$, así que
$$z^\prime=(1+i)(2+ i),$$
luego
$$
\begin{array}{rcl}
z&=&n\cdot z^\prime\cr
&=&3\cdot(2+i)\cdot (2-i)\cdot(1+i)\cdot (2+ i)\cr
&=&3\cdot(2+i)^2\cdot (2-i)\cdot(1+i).
\end{array}
$$
El siguiente gráfico nos muestra la distribución de los primos cercanos al origen en los enteros de Gauss.

Puedes usar la aplicación interactiva para explorar la distribución de los primos de Gauss en cuadrados de diferente tamaño centrados en el origen.
Ecuaciones diofánticas
A modo de ejemplo, vamos a estudiar aquí un par de ecuaciones diofánticas cuyas soluciones pasan por el estudio de los enteros de Gauss realizado anteriormente.
Al comienzo del tema de anillos nos habíamos planteado como motivación el solucionar la ecuación diofántica
$$x^2+y^2=5.$$
Ahora reemplazaremos el término independiente con un entero positivo $>1$ cualquiera.
Teorema
Dado $n\geq 2$, la ecuación diofántica
$$x^2+y^2=n$$
tiene solución si y solo si cualquier primo $p\equiv 3$ mod $4$ tiene exponente par en la factorización de $n$. Además, en dicho caso el número de soluciones es finito.
Prueba
La ecuación planteada equivale a encontrar los enteros de Gauss $x+iy$ tales que $|x+iy|^2=n$. Si $x+iy=\pi_1\cdots\pi_n$ es una factorización en $\mathbb Z[i]$ entonces $|x+iy|^2=|\pi_1|^2\cdots|\pi_n|^2$. Sabemos además, por la clasificación de los primos de Gauss, que $|\pi_i|^2$ puede ser $2$, un entero primo $p\equiv 1$ mod $4$ o $p^2$ donde $p\equiv 3$ mod $4$. Esto demuestra la necesidad de la condición del enunciado. También la suficiencia porque, si se cumple, basta tomar $x+iy$ como el producto de:
-
Un factor $1+i$ por cada $2$ que aparezca en la factorización de $n$.
-
Si $p\equiv 1$ mod $4$, un factor $\pi$ con $|\pi|^2=p$ por cada factor $p$ de $n$.
-
Si $p\equiv 3$ mod $4$, un factor $p$ por cada dos factores $p$ de $n$.
El conjunto de todas las soluciones se obtiene permitiendo reemplazar los $\pi$ del segundo apartado por sus conjugados y tomando los asociados de todas las soluciones particulares así obtenidas. En particular hay un número finito de soluciones.
$x^2+y^2=1170$
En este caso concreto $1170=2\cdot 3^2\cdot 5\cdot 13$. El único primo que vale $3$ módulo $4$ y que aparece en esta factorización es el propio $3$, con exponente par, por lo que la ecuación tiene solución. Una solución se corresponde con el entero de Gauss $x+iy$ obtenido al multiplicar los siguientes factores:
-
$1+i$ por aparecer un $2$.
-
$2+i$ por haber un $5$ y $2+3i$ por haber un $13$.
-
$3$ por el $3^2$ que aparece.
Es decir,
$$(1+i)(2+i)(2+3i)3=-21+27i.$$
Otras soluciones concretas se obtienen permitiendo reemplazar los factores del segundo apartado por sus conjugados,
$$\begin{array}{rcl}
(1+i)(2-i)(2+3i)3&=&9+33i,\cr
(1+i)(2+i)(2-3i)3&=&33+9i,\cr
(1+i)(2-i)(2-3i)3&=&27-21i.
\end{array}$$
El conjunto de todas las soluciones $x+iy$ son las cuatro anteriores y sus asociados, 16 en total:
$$
\begin{array}{rrrr}
-21+27i,&9+33i,&33+9i,&27-21i,\cr
-27-21i,&-33+9i,&-9+33i,&21+27i,\cr
21-27i,&-9-33i,&-33-9i,&-27+21i,\cr
27+21i,&33-9i,&9-33i,&-21-27i.
\end{array}
$$
La otra ecuación diofántica que vamos a considerar en este epígrafe es la ecuación de Pitágoras
$$x^2+y^2=z^2.$$
Sus soluciones positivas $x,y,z>0$ se denominan ternas pitagóricas y parametrizan los triángulos rectángulos con lados de medida entera.
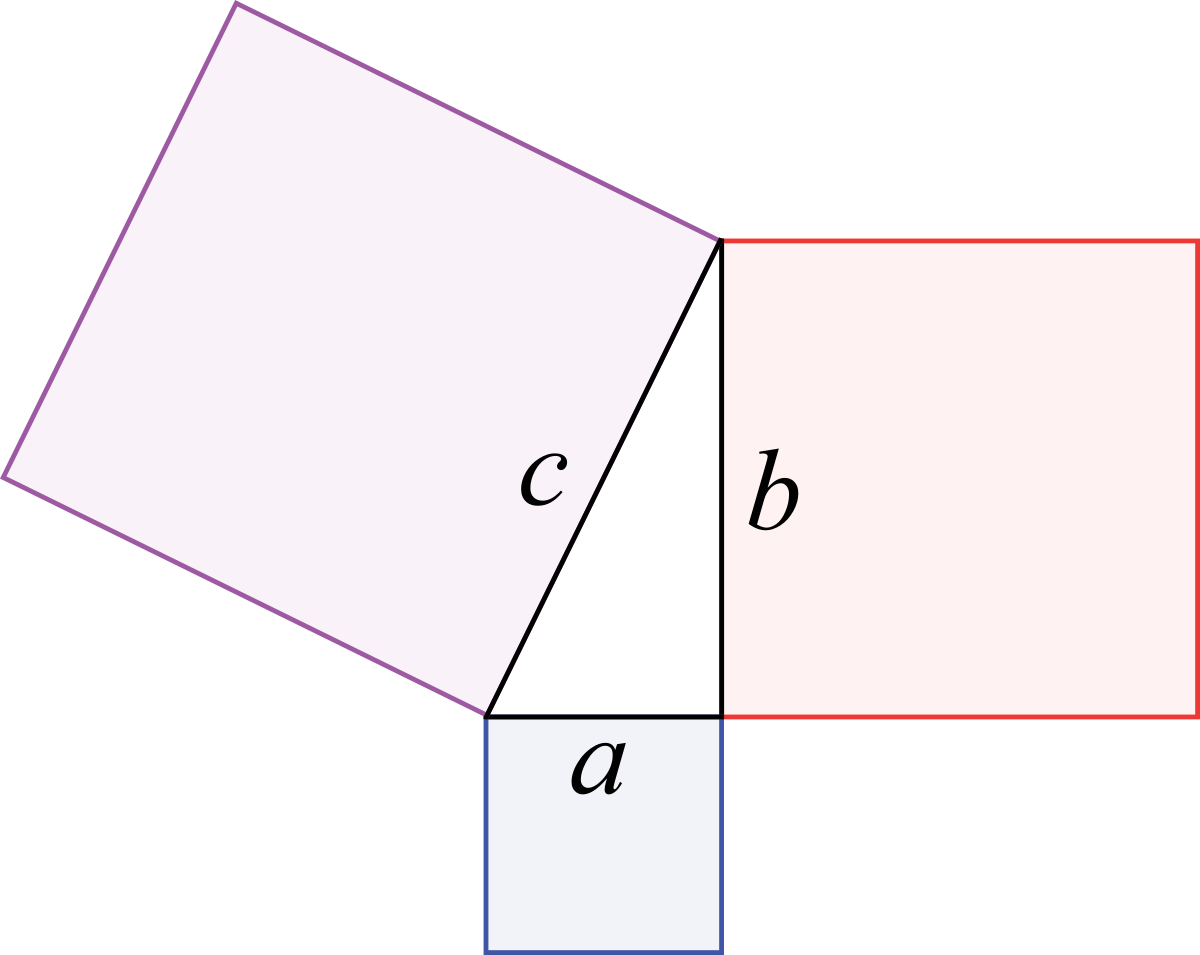
Los papeles de $x$ e $y$ en la ecuación de Pitágoras son intercambiables, por lo que $(x,y,z)$ es una solución si y solo si lo es
$$(y,x,z).$$
Los signos de las soluciones son irrelevantes, es decir si $(x,y,z)$ es una solución entonces también lo son
$$(\pm x,\pm y,\pm z).$$
Las soluciones triviales son las de la forma $(x,0,\pm x)$ o $(0,y,\pm y)$. Por tanto basta estudiar las ternas pitagóricas.
No hay ternas pitagóricas con $x$ e $y$ impares porque en ese caso $x\equiv\pm 1$ e $y\equiv \pm1$ mod $4$, así que $z^2=x^2+y^2\equiv 1+1=2$ mod $4$. Esto es imposible porque los únicos cuadrados en $\mathbb Z/(4)$ son $0$ y $1$.
Si $(x,y,z)$ es una terna pitagórica y $d=\operatorname{mcd}(x,y)$ entonces $d^2|x^2$ y $d^2|y^2$ por lo que $d^2|z^2$. Por tanto $d|z$ y
$$\left(\frac{x}{d},\frac{y}{d},\frac{z}{d}\right)$$
es otra terna pitagórica con $\operatorname{mcd}(\frac{x}{d},\frac{y}{d})=1$. En definitiva, podemos centrarnos en buscar las ternas pitagóricas $(x,y,z)$ tales $\operatorname{mcd}(x,y)=1$. Estas se denominan ternas pitagóricas primitivas. Las que no son primitivas se obtienen a partir de las primitivas multiplicando por enteros positivos. En una terna pitagórica primitiva $x$ e $y$ no pueden ser ambos pares. A la luz del párrafo anterior, $x$ ha de ser par e $y$ impar, o viceversa, es decir,
$$x\not\equiv y \mod 2.$$
Podemos pues suponer que $x$ es impar e $y$ es par, el resto de ternas pitagóricas primitivas se obtendrán intercambiando la $x$ y la $y$.
La conexión de la ecuación de Pitágoras con los enteros de Gauss proviene de que esta ecuación equivale a
$$(x+iy)(x-iy)=z^2.$$
Lema
Dados $x,y\in\mathbb Z$ no nulos, tenemos que $x\equiv y$ mod $2$ $\Leftrightarrow$ $(1+i)|(x+iy)$.
Prueba
$\Rightarrow$ Si $x\equiv y$ mod $2$ entonces $x$ e $y$ son ambos pares o ambos impares. Si son ambos pares entonces $2|(x+iy)$ y ya sabemos que $(1+i)|2$ con lo que $(1+i)|(x+iy)$. Si son ambos impares entonces $y\pm x$ es par y tenemos la siguiente ecuación en $\mathbb Z[i]$,
$$x+iy=(1+i)\left(\frac{y+x}{2}+i\frac{y-x}{2}\right).$$
$\Leftarrow$ Si $(1+i)|(x+iy)$ entonces
$$x+iy=(1+i)(x^\prime+iy^\prime)=(x^\prime-y^\prime)+(x^\prime+y^\prime)i$$
y por tanto
$$x=x^\prime-y^\prime\equiv x^\prime+y^\prime=y \mod 2.$$
En el siguiente lema caracterizamos en términos de los enteros de Gauss la condición sobre $x$ e $y$ que caracteriza las ternas pitagóricas que son primitivas.
Lema
Dados $x,y\in\mathbb Z$ no nulos, tenemos que $\operatorname{mcd}(x,y)=1$ y $x\not\equiv y$ mod $2$ $\Leftrightarrow$ $\operatorname{mcd}(x+iy,x-iy)=1$.
Prueba
$\Rightarrow$ Por reducción al absurdo. Si $\pi\in\mathbb Z[i]$ es un primo de Gauss tal que $\pi|(x+iy)$ y $\pi|(x-iy)$ entonces
$$\begin{array}{rcl}\pi \mid [(x+iy)+(x-iy)]&=&2x,\cr \pi \mid [(x+iy)-(x-iy)]&=&2yi.\end{array}$$
El primo $\pi$ no puede dividir simultáneamente a $x$ y a $y$ ya que $\operatorname{mcd}(x,y)=1$, y el máximo común divisor de dos enteros es el mismo calculado en $\mathbb{Z}$ o en $\mathbb{Z}[i]$. De aquí deducimos que $\pi|2$, es decir $\pi=1+i$ (o un asociado). Por tanto $(1+i)|(x+iy)$, así que por el lema anterior $x\equiv y$ mod $2$, lo cual es una contradicción.
$\Leftarrow$ Cualquier divisor común de $x$ e $y$ divide tanto a $x+iy$ como a $x-iy$, por tanto $\operatorname{mcd}(x,y)=1$. Además $x\not\equiv y$ mod $2$ ya que en caso contrario, por el lema anterior, $(1+i)|(x+iy)$ y por tanto $(1-i)|(x-iy)$. Como $1+i$ y $1-i$ son asociados, ambos dividirían tanto a $x+iy$ como a $x-iy$, que no podrían ser coprimos.
Lema
En un DFU $R$, las soluciones no nulas de la ecuación $xy=z^2$ tales $\operatorname{mcd}(x,y)=1$ son, salvo asociados, todas de la forma $x=a^2$, $y=b^2$ y $z=ab$ con $a,b\in R$, $\operatorname{mcd}(a,b)=1$.
Prueba
Si $z$ fuera una unidad, entonces también lo tendrían que ser $z^2$, $x$ e $y$, por tanto, salvo asociados, $x=y=z=1=1^2$. Supongamos ahora que $z$ no es una unidad. Sea $z=p_1\cdots p_n$ una factorización como producto de primos. Como $xy=z^2=p_1^2\cdots p_n^2$, por la unicidad de las factorizaciones en $R$ los factores primos de $z^2$ se han de repartir entre $x$ e $y$, salvo asociados. Además, como $\operatorname{mcd}(x,y)=1$, los dos factores de cada $p_i^2$ tienen que quedar del mismo lado, por lo que tanto $x$ como $y$ son cuadrados, $x=a^2$ e $y=b^2$, y $z=ab$, de nuevo salvo asociados. Además $\operatorname{mcd}(a,b)=1$ porque $1=\operatorname{mcd}(x,y)=\operatorname{mcd}(a,b)^2$.
Teorema
Las ternas pitagóricas primitivas con segunda coordenada par son las de la forma $(a^2-b^2, 2ab, a^2+b^2)$ con $a,b\in\mathbb Z$, $a>b>0$, $\operatorname{mcd}(a,b)=1$, $a\not\equiv b$ mod $2$.
Prueba
La ecuación de Pitágoras, vista en $\mathbb Z[i]$, es
$$(x+iy)(x-iy)=z^2.$$
Según hemos visto mas arriba, la condición de que una terna pitagórica sea primitiva equivale a $\operatorname{mcd}(x+iy,x-iy)=1$. Por el lema anterior, tanto $x+iy$ como $x-iy$ son cuadrados, o asociados de cuadrados, necesariamente conjugados. Es decir, $x+iy=u(a+ib)^2$ para cierto $u=1,-1,i,-i$. Esto da lugar a las siguientes posibilidades:
$$
(x,y)=\left\{\begin{array}{l}
(a^2-b^2,2ab),\cr
(b^2-a^2,-2ab),\cr
(-2ab,a^2-b^2),\cr
(2ab,b^2-a^2).
\end{array}\right.
$$
Las dos últimas no dan lugar al tipo de terna pitagórica primitiva que estamos considerando, pues $x$ sería par. La primera sí, siempre que $a>b>0$, pues $x,y>0$. También si $ a < b < 0$, pero por este camino llegaríamos a las mismas ternas. La segunda posibilidad también da lugar a las mismas ternas que la primera. Así que podemos suponer que $x+iy=(a+ib)^2$ con $a>b>0$ y por tanto $x-iy=(a-ib)^2$.
De nuevo por el lema anterior,
$$z=u(a+ib)(a-ib)=u(a^2+b^2)$$
para cierta unidad $u\in\{\pm1,\pm i\}$. Como la ecuación $(x+iy)(x-iy)=z^2$ ha de satisfacerse, la unidad ha de ser tal que $u^2=1$, con lo que $u=\pm 1$. El caso $u=-1$ lo excluimos ya que entonces $z=-(a^2+b^2)<0$, por tanto $z=a^2+b^2$. Además, una vez más por el lema anterior, $\operatorname{mcd}(a+ib,a-ib)=1$, es decir $\operatorname{mcd}(a,b)=1$ y $a\not\equiv b$ mod $2$, usando el lema de más arriba. Esto reduce todas las posibilidades a las que aparecen en el enunciado del teorema. Veamos que todas ellas son en efecto ternas pitagóricas primitivas.
Claramente, las ternas del enunciado resuelven la ecuación de Pitágoras, es decir,
$$(a^2-b^2)^2+(2ab)^2=(a^2+b^2)^2.$$
Las tres coordenadas son positivas, pues $a>b>0$. La segunda coordenada es claramente par. Solo queda comprobar que las dos primeras son coprimas. Para ello, demostraremos que la primera no es divisible por $2$ ni por ningún factor primo de $a$ o de $b$. Como $n\equiv n^2$ mod $2$ para todo $n\in\mathbb{Z}$, $a^2-b^2\equiv a-b\not\equiv 0$ mod $2$, pues $a\not\equiv b$ mod $2$, así que $a^2-b^2$ es impar. Sea $p\in\mathbb{Z}$ un primo. Si $p\mid a$ entonces $p\mid a^2$. Si fuera cierto que $p\mid (a^2-b^2)$ entonces tendriamos que $p\mid b^2$ y por tanto $p\mid b$. Esto contradeciría que $\operatorname{mcd}(a,b)=1$, luego en realidad $p\nmid (a^2-b^2)$. Análogamente se prueba que si $p\mid b$ entonces $p\nmid (a^2-b^2)$. Esto concluye la demostración.
El siguiente gráfico muestra los pares $(x,y)$ que forman parte de una terna pitagórica cualquiera con $x,y\leq 4500$.

Explora la distribución de las ternas pitagóricas primitivas en el plano con la aplicación interactiva diseñada para dicho propósito.


